We'll use implicit differentiation:
Let #y = "arccot"(x)#
#=> cot(y) = x#
#=> d/dxcot(y) = d/dxx#
#=> -csc^2(y)dy/dx = 1#
#=> dy/dx = -1/csc^2(y)#
Now let's see what #csc^2(y)# is in terms of #x#. Draw a right triangle with an angle #y# such that #cot(y) = x# (i.e. #y= "arccot"(x)#):
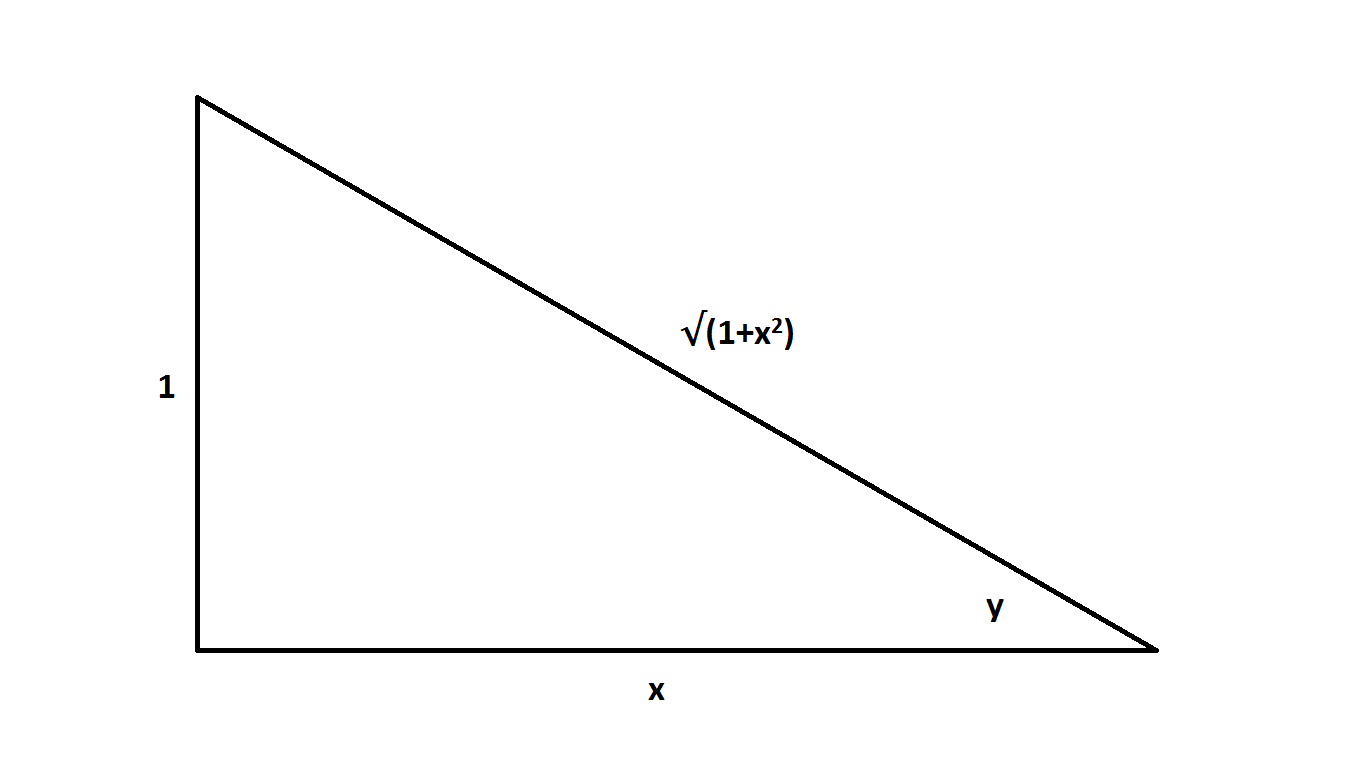
Setting the legs so that #cot(y) = x#, we can find the length of the hypotenuse as #sqrt(1+x^2)# using the Pythagorean theorem. Now we can calculate #csc^2(y)#.
#csc^2(y) = (csc(y))^2 = (sqrt(1+x^2)/1)^2 = 1+x^2#
Substituting this in, we arrive at our answer:
#("arccot"(x))' = dy/dx = -1/(1+x^2)#



