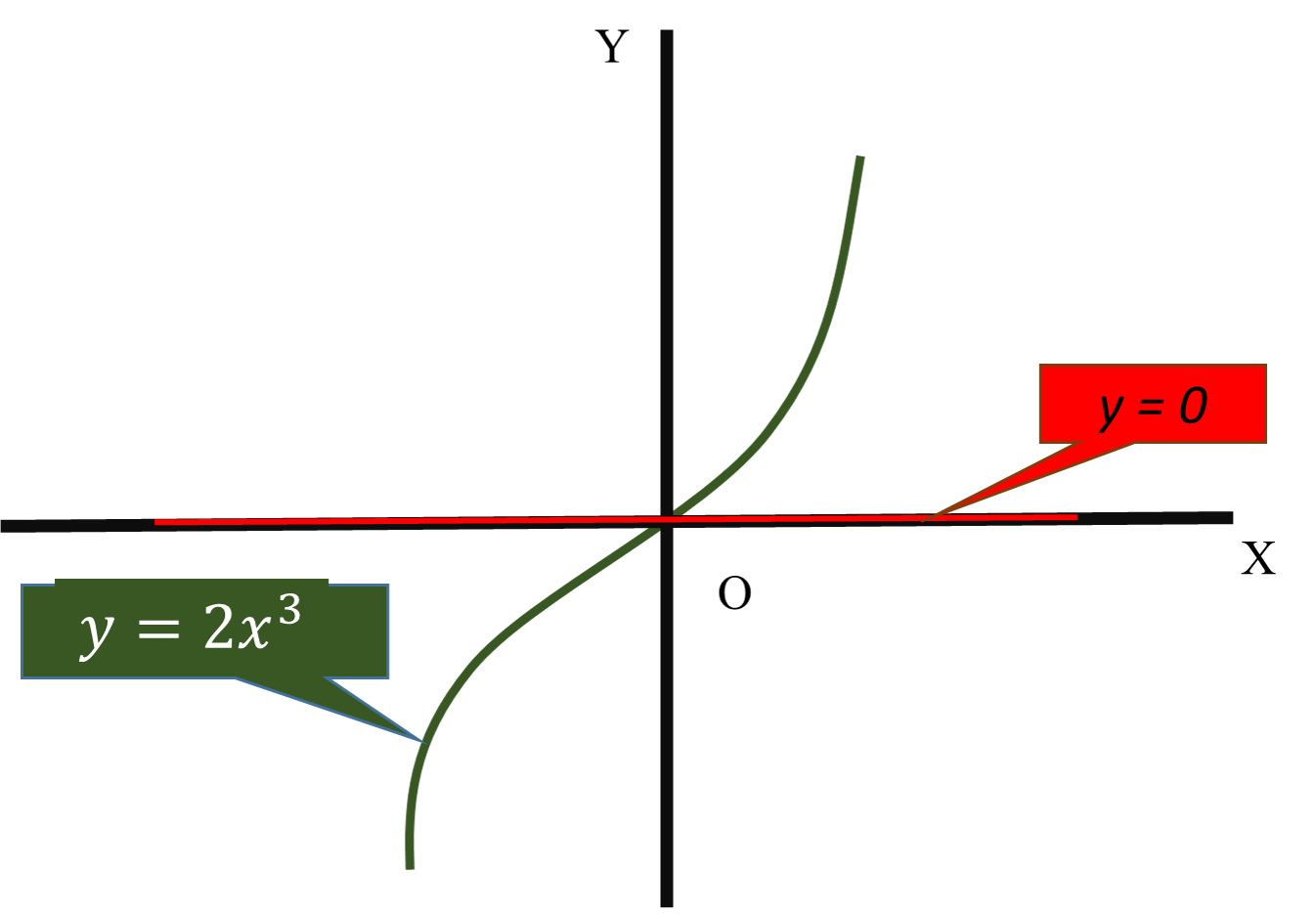
How do you find the points where the graph of the function #y=2x^3# has horizontal tangents and what is the equation?

Question

2229 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-24T05:18:29

#y=0#

Given -

#y=2x^3#

It is a cubic function.

It has no constant terms. Hence it passes through the origin.

The slope of a horizontal tangent is #0#

We have to find for which value of #x# the slope of the curve becomes zero.

The first derivative of the function gives the slope of the curve at any given point on the curve.

#dy/dx=6x^2#

#dy/dx=0 => 6x^2=0#

#x=0#

When #x# takes the value #0# the slope of the curve is zero.

The tangent is through #(0,0)#

Hence the equation of the tangent is #y=0#

enter image source here