Graph #f(x)=x^4-4# using zeros and end behavior.
To find the zeros, factor the polynomial.
#f(x)=(x^2-2)(x^2+2)#
Factor again.
#f(x)=(x+sqrt2)^color(red)1(x-sqrt2)^color(red)1(x^2+2)#
Setting each factor equal to zero and solving gives:
#x=-sqrt2#, #x=sqrt2# and #x=+-sqrt2i#
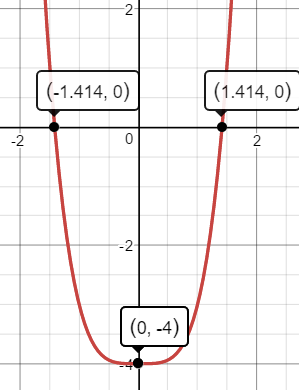
The only real zeros are #sqrt2# and #-sqrt2#. Each has a multiplicity of #color(red)1# because the exponent on each factor is #color(red)1#. An odd multiplicity means the graph crosses (or cuts through) the #x# axis at the zeros/x-intercepts. The #x# intercepts are #(-sqrt2,0)# and #(sqrt2, 0)# which are approximately #(+-1.414,0)#.
To find the end behavior, examine the degree and leading coefficient of the original polynomial.
#f(x)=color(blue)1x^color(violet)4-4#
The degree is #color(violet)4# and the leading coefficient is #color(blue)1#.
An even degree with a positive leading coefficient indicates that as#xrarroo# and #xrarr-oo#, #f(x)rarroo#. In other words, the "ends" of the graph both point "up".
It is also helpful to find the #y# intercept. Setting #x=0# gives
#y=0^4-4=-4#. The #y# intercept is #(0, -4)#
The graph is shown below.