How do you find the equation of a line tangent to the function #y=x^2-2# at x=0?
1 Answer
Explanation:
If
When
so the tangent passes through
Using
It should also be obvious that
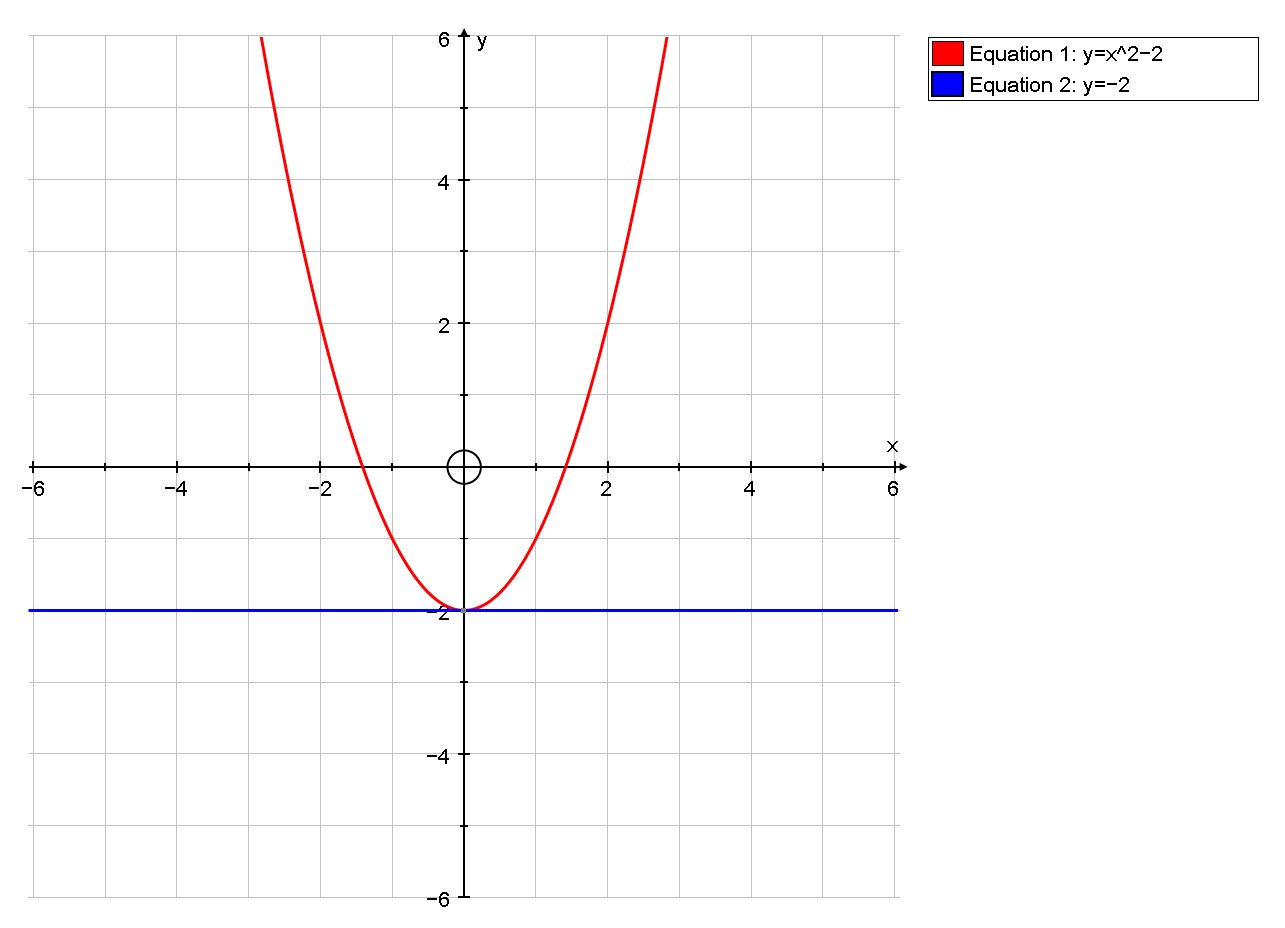
If
When
so the tangent passes through
Using
It should also be obvious that
