Question

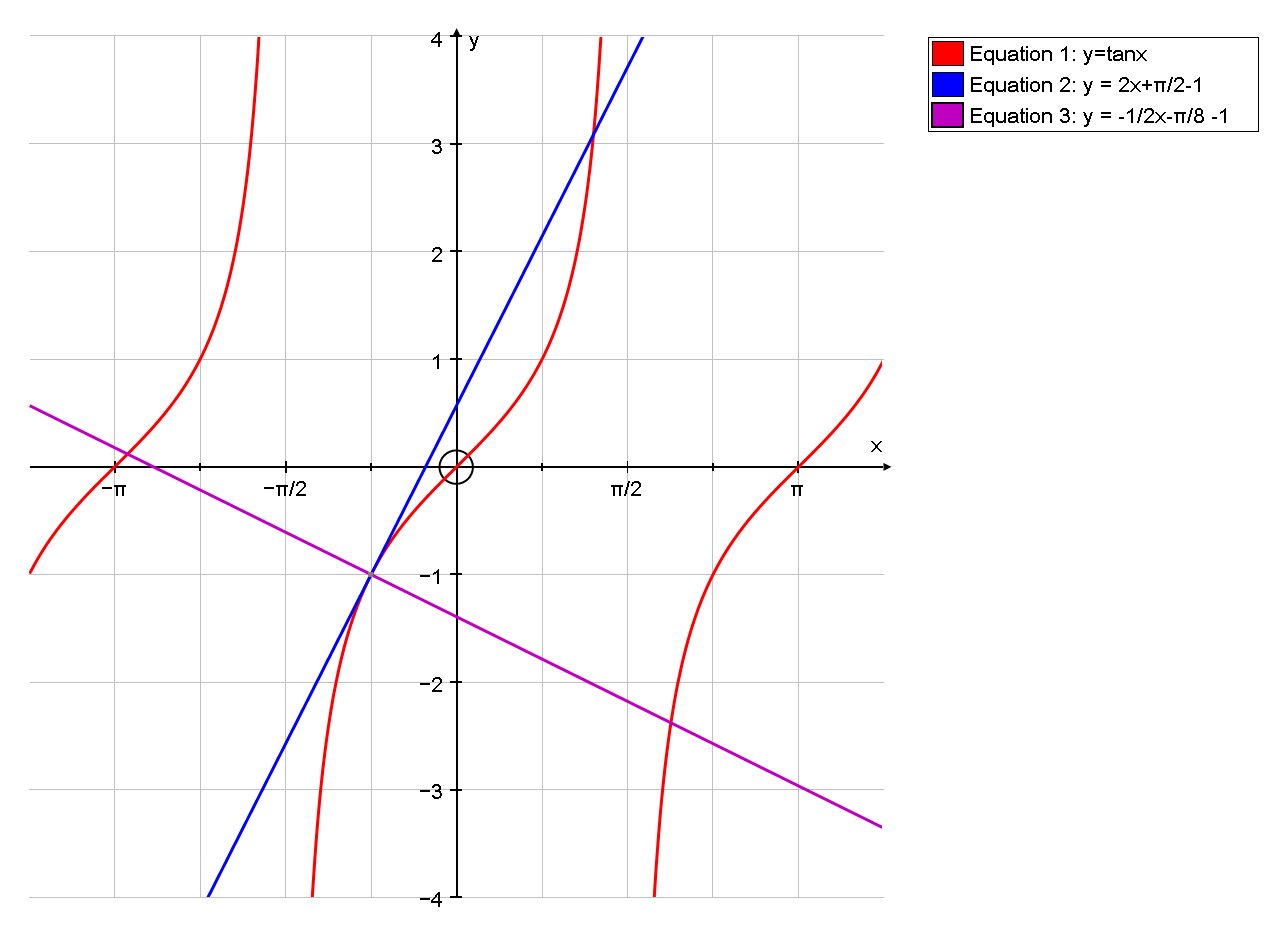
How do you find the equation of the tangent and normal line to the curve `y=tanx` at `x=-pi/4`?

Answer 1

Tangent: `y = 2x+pi/2-1`
Normal: `y = -1/2x-pi/8 -1`

Explanation:

The gradient tangent to a curve at any particular point is given by the derivative.

If `y=tanx` then `dy/dx=sec^2x`

When `x=-pi/4`
`=> y=tan(-pi/4)=-1`
`=> dy/dx=sec^2(-pi/4)=2`

So the tangent passes through `(-pi/4,-1)` and has gradient `m_T=2`

Using `y-y_1 = m(x-x_1)` the equation of the tangent is:

`y-(-1) = (2)(x-(-pi/4))`
`:. y+1 = 2x+pi/2`
`:. y = 2x+pi/2-1`

The normal is perpendicular to the tangent, so the product of their gradients is -1 hence normal passes through `(-pi/4,-1)` and has gradient `m_N=-1/2`

so the equation of the normal is:

`y-(-1) = -1/2(x-(-pi/4))`
`:. y+1 = -1/2x-pi/2`
`:. y = -1/2x-pi/8 -1`