Question

How do you find the equation of the tangent line to the curve `y=x^4+2x^2-x` at (1,2)?

Answer 1

`y = 7x - 5`

Explanation:

We have; `y = x^4 + 2x^2 - x`

First we differentiate wrt `x`;
`y = x^4 + 2x^2 - x`
`:. dy/dx = 4x^3 + 4x - 1`

We now find the vale of the derivative at `(1,2)` (and it always worth a quick check to see that `y=2` when `x=1`) we have `dy/dx=4+4-1=7`

So at the tangent passes through the coordinate `(1,2)` and has gradient `m=7`

We now use `y-y_1 = m(x-x_1)` to get the equation of the tangent:

`:. y - 2 = 7 (x - 1)`
`:. y - 2 = 7x - 7`
`:. y = 7x - 5`

Answer 2

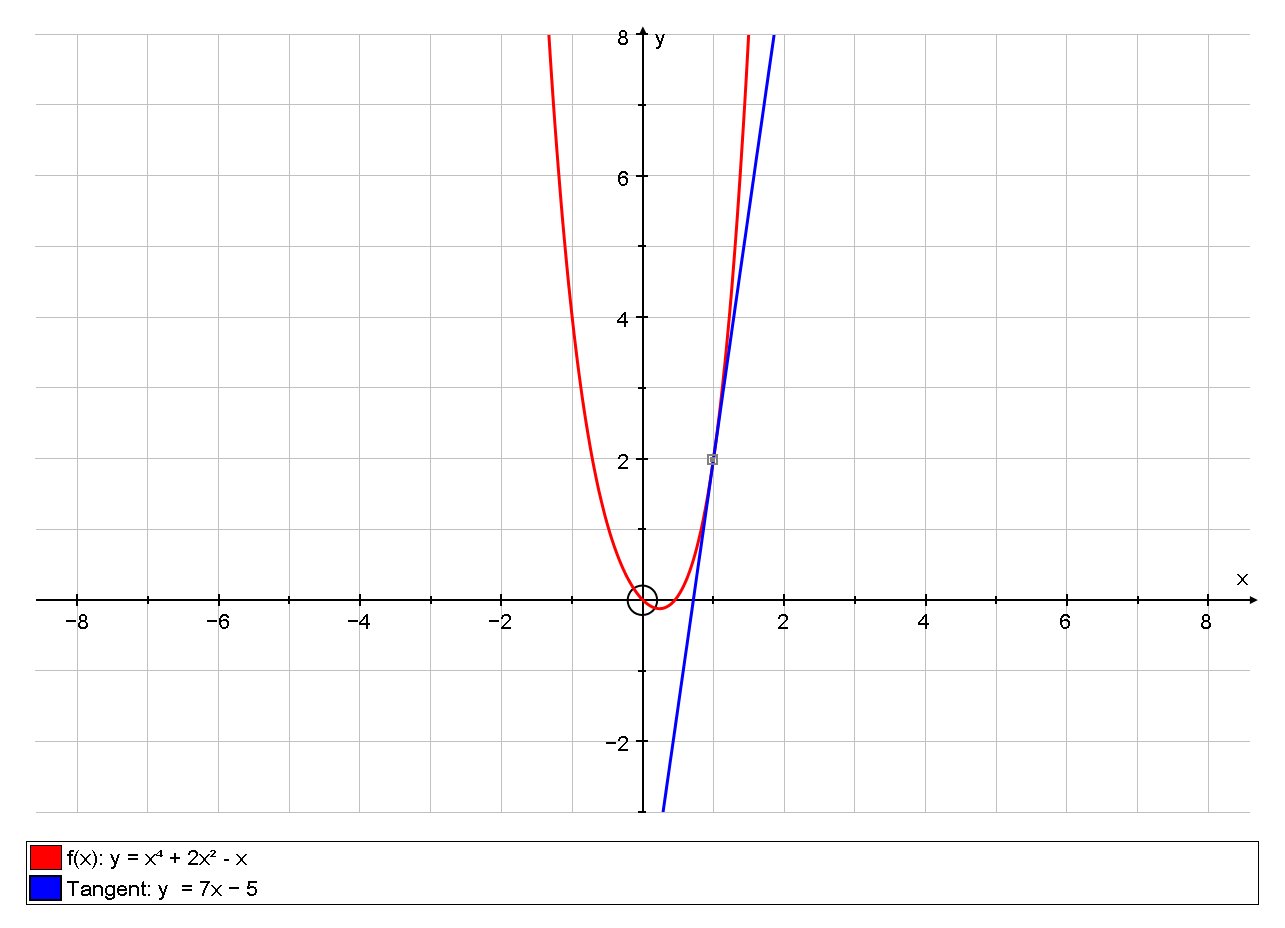
The equation of the tangent is `y=7x-5`

Explanation:

let `f(x)=x^4+2x^2-x`
Then the derivative is `f'(x)=4x^3+4x-1`

At the point `(1,2)`, `f'(1)=4+4-1=7`

So the slope of the tangent is `m=7`
The equation of the line is, `y-2=7(x-1)`
`y-7x=-5`
graph{(y-x^4-2x^2+x)(y-7x+5)=0 [-5.55, 5.55, -2.773, 2.776]}