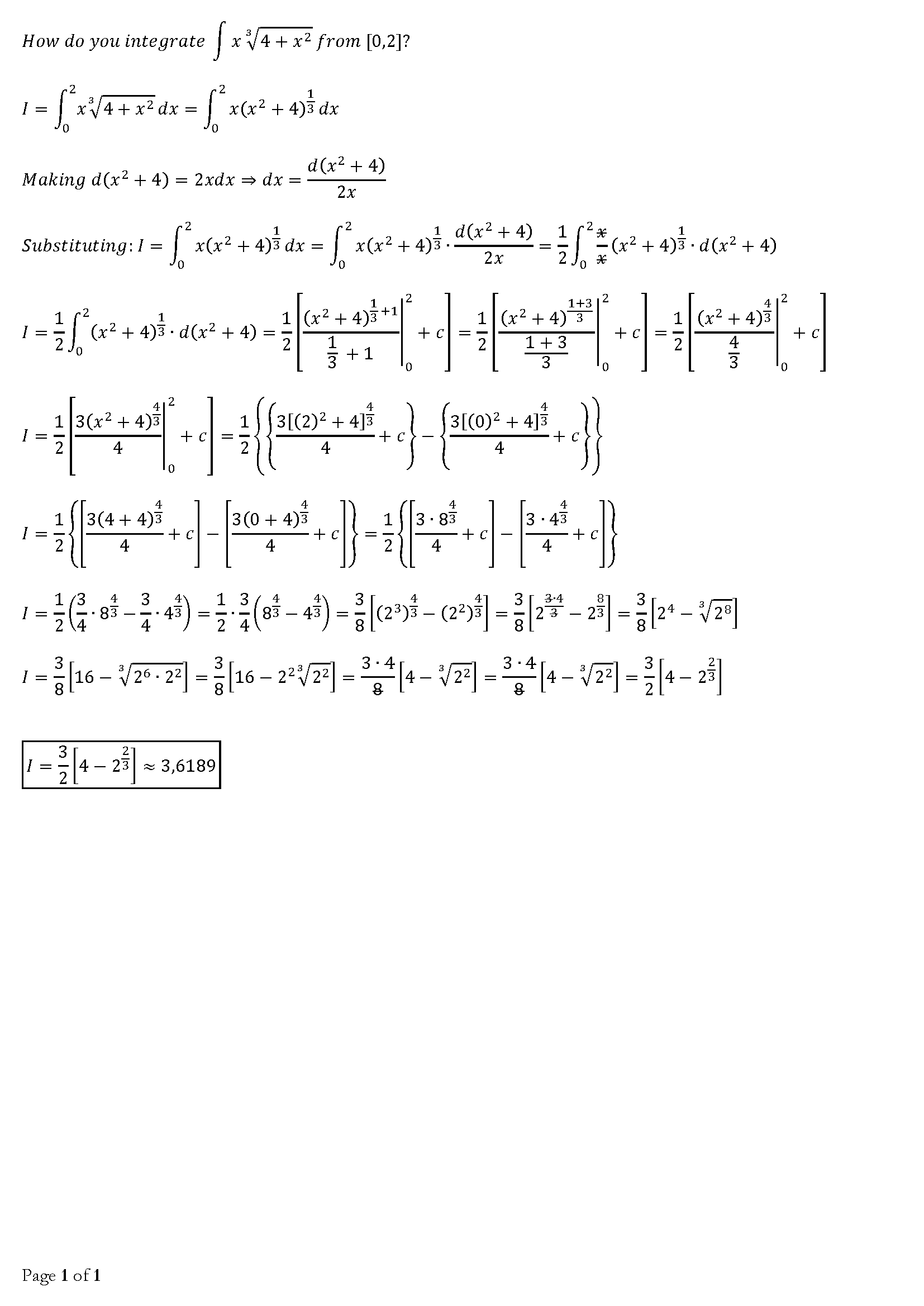How do you integrate int xroot3(4+x^2) from [0,2]?
2 Answers
Nov 11, 2016
The answer is
Explanation:
Use the substitution,
so,
So
Nov 11, 2016
See answer below: