How do you find the equation of the tangent line to the graph of #f(x)=x^3# at point (2,8)?
2 Answers
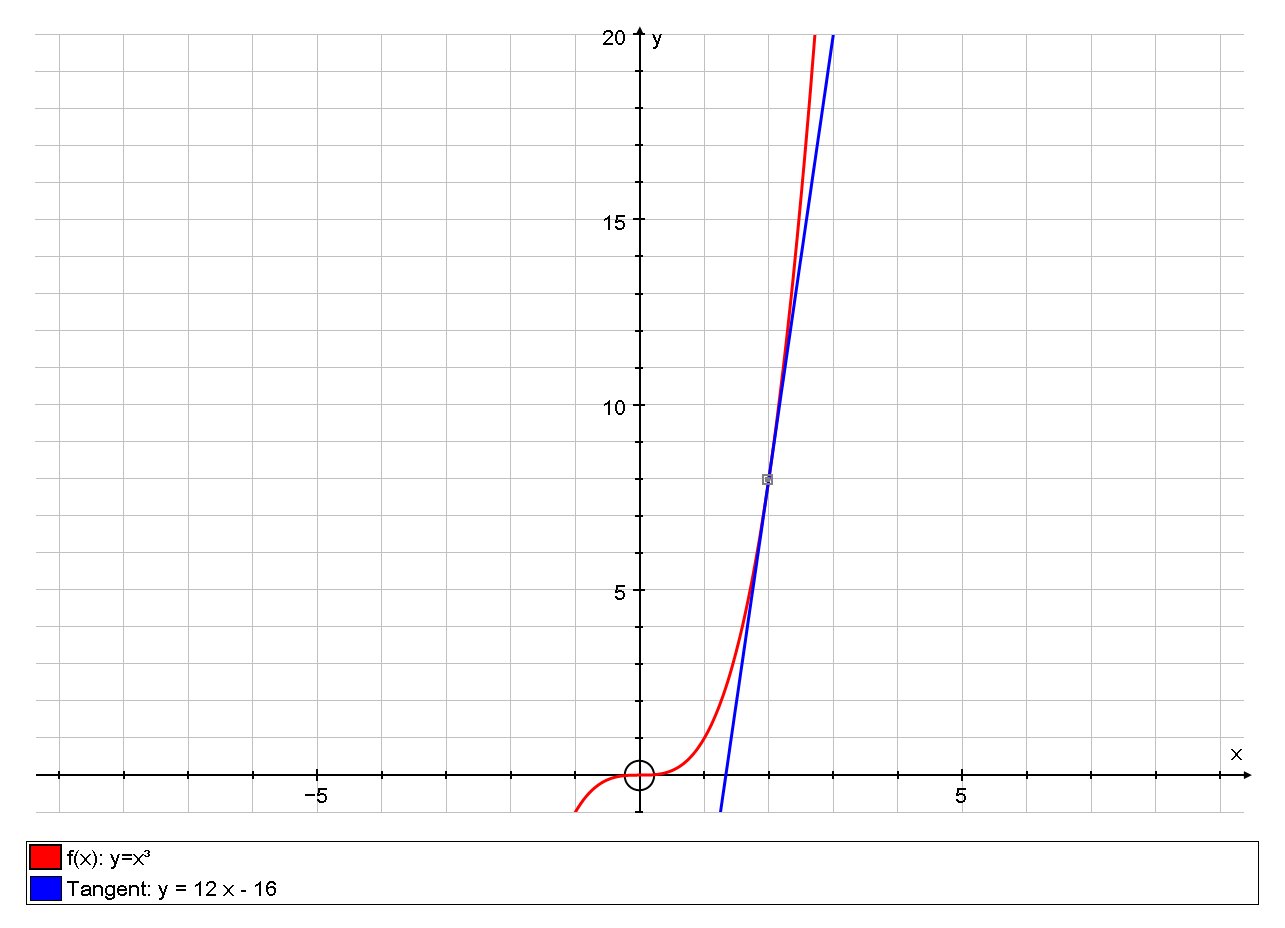
# y = 12 x - 16 #
Explanation:
The gradient of the tangent at any particular point is given by the derivative.
# f(x) = x^3 #
# :. f'(x) = 3x^2 #
At
So the tangent passes through
So, Using
# y - 8 = 12( x - 2 ) #
# :. y - 8 = 12 x - 24 #
# :. y = 12 x - 16 #
The method you use to find the slope of the tangent line depends on your current studies.
Explanation:
If you have learned the power rule for derivatives, use that. If you are using the definition (or an equivalent), then the details depend on the definition (or equivalent) you use.
Two likely definitions are
The slope of the line tangent to the graph of function
In this question, we have
Using the first version
# = lim_(hrarr0)(8+12h+6h^2+h^3- 8)/h #
# = lim_(hrarr0)(12h+6h^2+h^3)/h #
# = lim_(hrarr0)(cancel(h)(12+6h+h^2))/cancel(h) #
# = 12 + 6(0)+(0)^2 = 12#
Using the second version
# = lim_(trarr2)(t^3- 8)/(t-2)#
# = lim_(trarr2)(cancel((t-2))(t^2+2t+4))/cancel(t-2)#
# = (2)^2+2(2)+4 = 4+4+4=12#
Now that we have the slope, we can do the algebra to find an equation for the line through


