How do you find all critical point and determine the min, max and inflection given #f(x)=x^3+x^2-x#?
2 Answers
Critical Points are:
Explanation:
We have
To identify the critical vales, we differentiate and find find values of
Differentiating wrt
# f'(x) = 3x^2 + 2x - 1 # .... [1]
At a critical point,
# f'(x)=0 => 3x^2 + 2x - 1 = 0 #
# :. (3x-1)(x+1) = 0 #
# x=-1,1/3 #
Ton find the y-coordinate we substitute the required value into
So the critical points are
We identify the nature of these critical points by looking at the sign of second derivative, and
Differentiating [1] wrt
# f''(x) = 6x + 2 #
# x=-1 => f''(-2)=-6+2 < 0 # , ie a maximum
# x=1/3 => f''(1)= 2+2>0# , ie a minimum
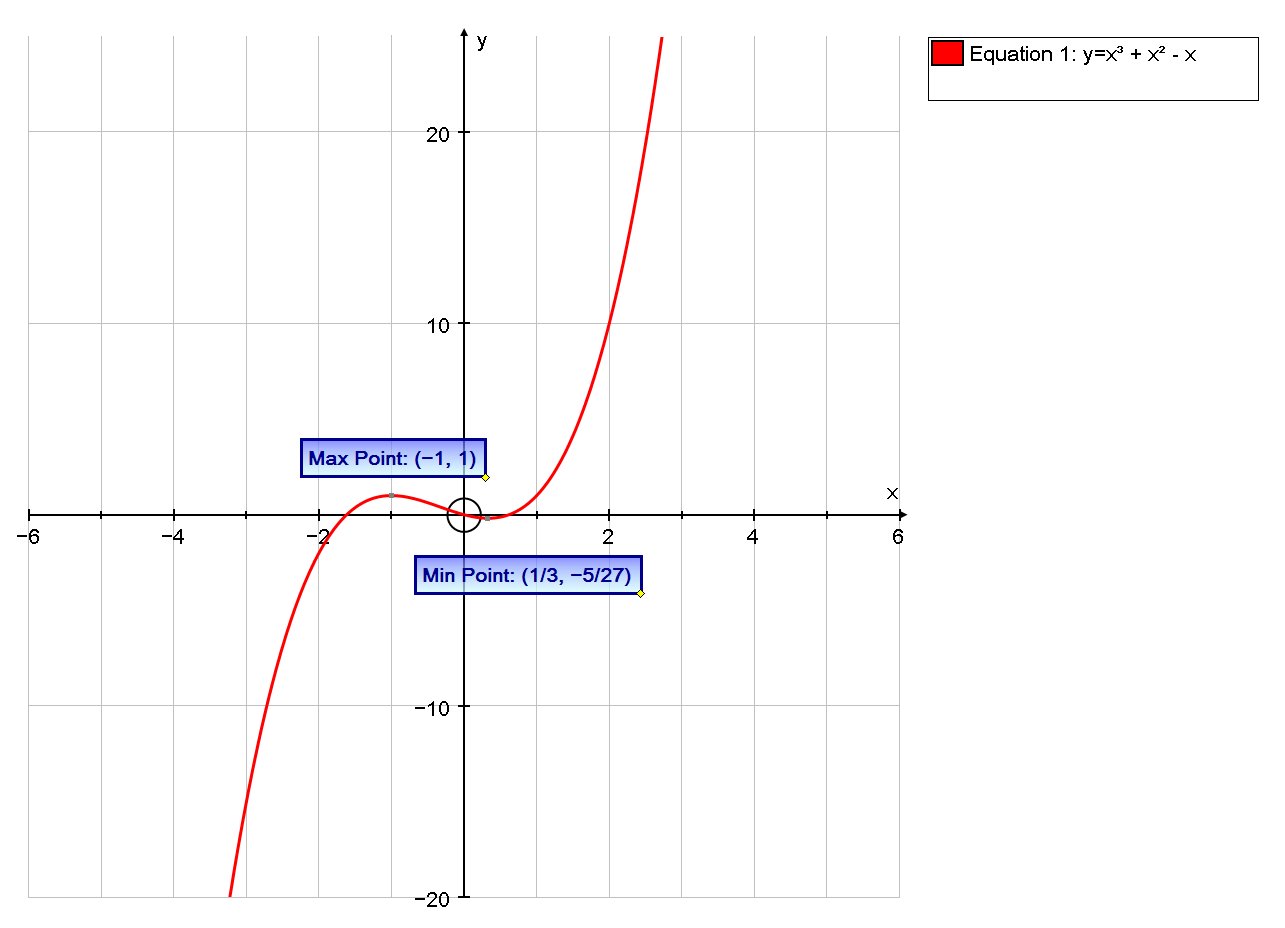
Incidental, As this is a cubic with a positive coefficient of
The max is at
The min is at
The inflexion point is at
Explanation:
We have to calculate the first and second derivative.
So, we do a sign chart
So, we have a max at
To determine the inflexion points, we calculate
The inflexion point is at
Also,
and
graph{x^3+x^2-x [-2.43, 2.436, -1.217, 1.215]}


