Question

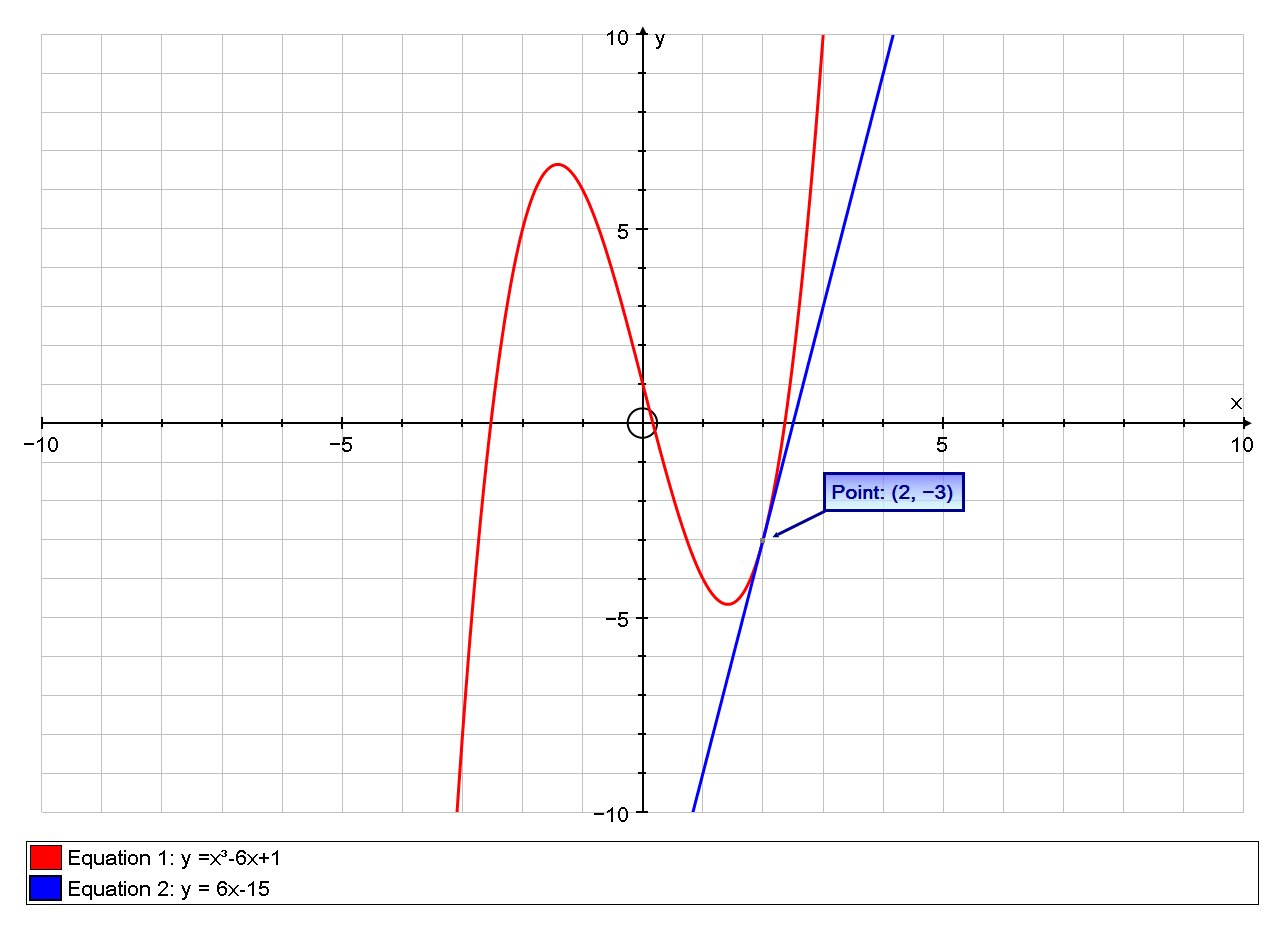
How do you find the equation of a line tangent to the function `y=x^3-6x+1` at x=2?

Answer 1

`y = 6x-15`

Explanation:

We have

`y =x^3-6x+1`

The gradient of the tangent at any particular point is given by the derivative: So differntiating wrt `x` we have,

`dy/dx=3x^2-6`

When `x=2 => y=8-12+1=-3`
And, `dy/dx = (3)(4)-6=6`

So the tangent passes through `(2,-6)` and has gradient `m=6`, so using the equation `y-y_1=m(x-x_1)` the tangent equation is:
`y-(-3) = 6(x-2)`
`:. y+3 = 6x-12`
`:. y = 6x-15`