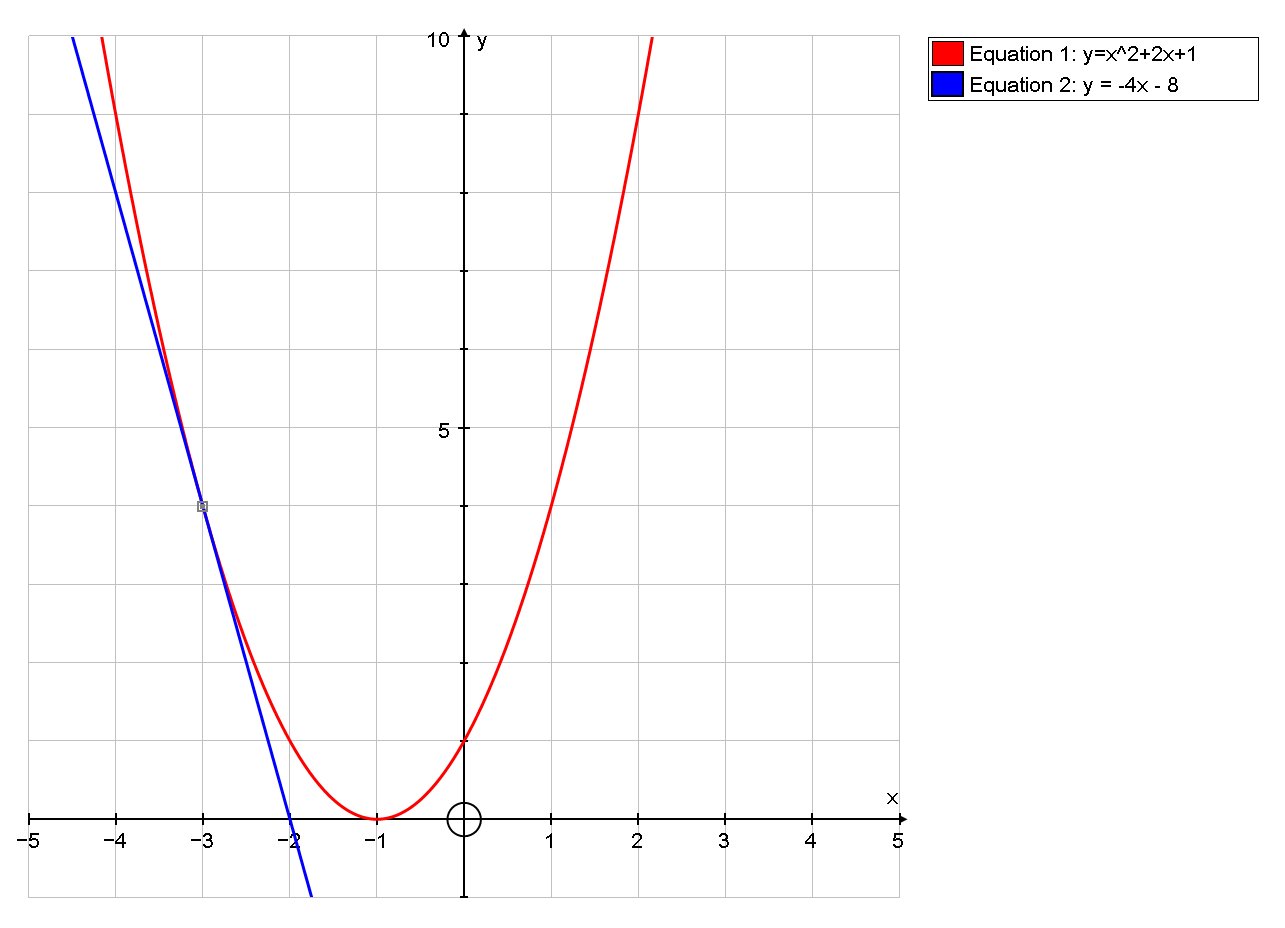
How do you find the equation of the tangent line to the graph of #f(x)=x^2+2x+1# at point (-3,4)?

Question

16259 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-18T02:31:49

# y = -4x - 8 #

The gradient of tangent to a function at any particular point is given by the derivative at that point.

Now:

# f(x)=x^2+2x+1#

Differentiating wrt #x# we get;

# f'(x)=2x+2#

When # x=-3 => f(-3)=9-6+1=4# (Confirming that #(-3,4)# lies on the curve), And, #f'(-3)=-6+2=-4#

So the required tangent passes through #(-3,4)#, and has gradient #m=-4#. So using #y=y_1=m(x-x_1)#, the required equation is;

# y-4 = -4(x-(-3)) #
# :. y-4 = -4x - 12 #
# :. y = -4x - 8 #

enter image source here