Question

A triangle has corners at `(-4 ,2 )`, `(7 ,1 )`, and `(2 ,-7 )`. If the triangle is dilated by a factor of `2/5` about point #(-1 ,4 ), how far will its centroid move?

Answer 1

the centroid will move by about `(8sqrt(5))/5`
`Delta=(8sqrt(5))/5`

`Delta=3.5771" "`units

Explanation:

the solution:

the centroid of the given triangle is at
`x_o=(-4+7+2)/3=5/3`

`y_o=(2+1-7)/3=-4/3`

the reference point is at `(-1, 4)" "`and scale factor `k=2/5`

Let the unknown new centroid be at `C(x_c, y_c)`

By segment division method

`(x_c-(-1))/(x_o-(-1))=2/5`

`(x_c-(-1))/(5/3-(-1))=2/5`

`x_c=1/15`

Also

`(y_c-4)/(y_o-4)=2/5`

`(y_c-4)/(-4/3-4)=2/5`

`y_c=28/15`

The old centroid is at `(5/3, -4/3)" "`(black colored dot)
The new centroid is at `C(1/15, 28/15)" "`(orange colored dot)

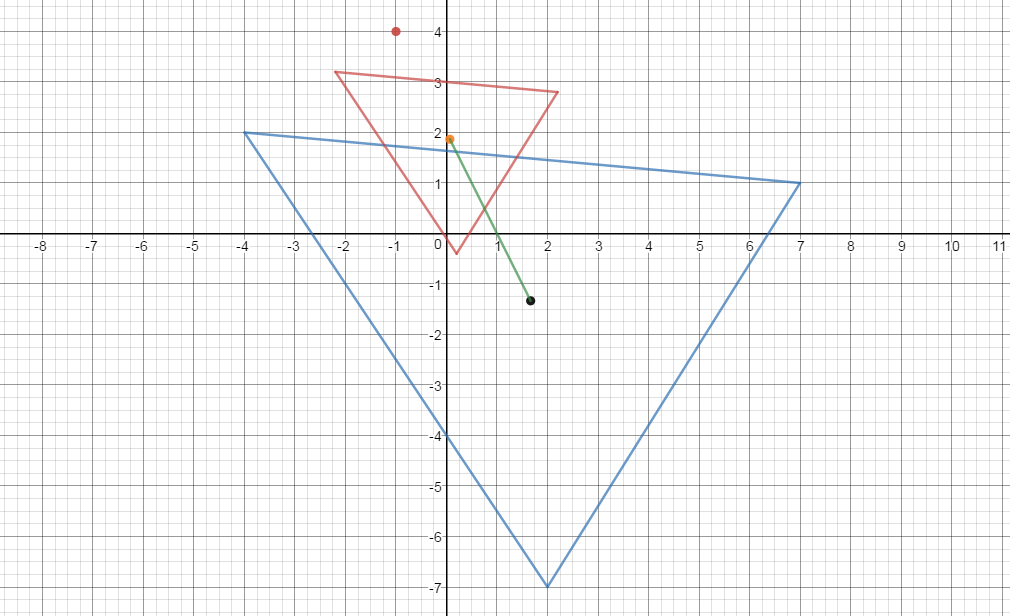
how far did the centroid move ?

`Delta=sqrt((x_o-x_c)^2 + (y_o-y_c)^2)`

`Delta=sqrt((5/3-1/15)^2 + (-4/3-28/15)^2)`

`Delta=sqrt((64+256)/25)`

`Delta=(8sqrt(5))/5`

`Delta=3.5771" "`units (length of the green segment)

God bless.... I hope the explanation is useful.