How do you find the local maximum and minimum values of g(x)=x^3+5x^2-17x-21?
1 Answer
Nov 30, 2016
Local Maximum :
Local Minimum :
Explanation:
From the given equation
take the first derivative
Set
to values for x:
and
Solve for corresponding values of y using
Local Maximum:
Local Minimum :
Kindly see the graph below for better view
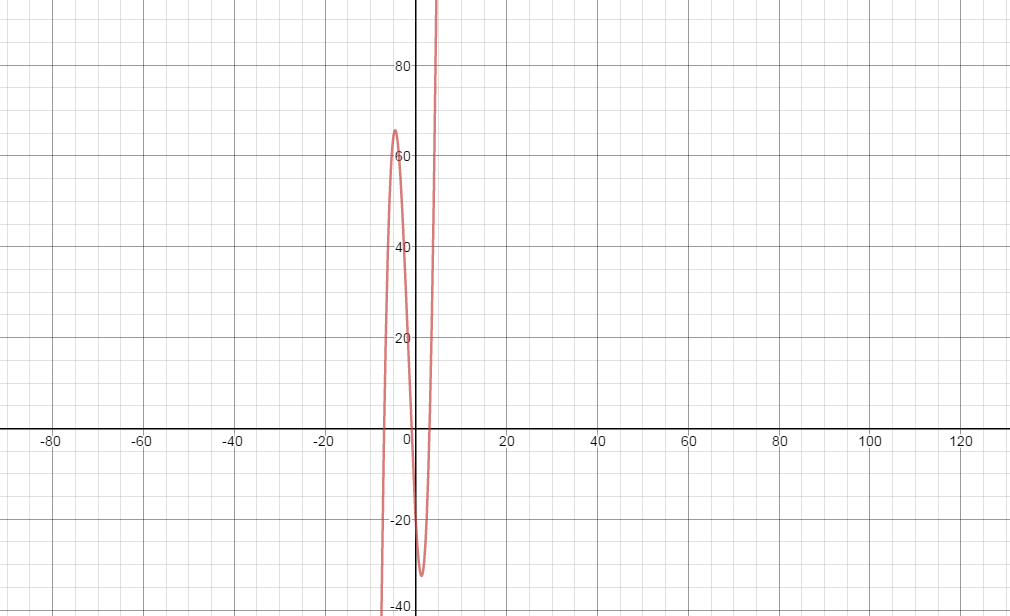 Desmos.com
Desmos.com
God bless....I hope the explanation is useful.
