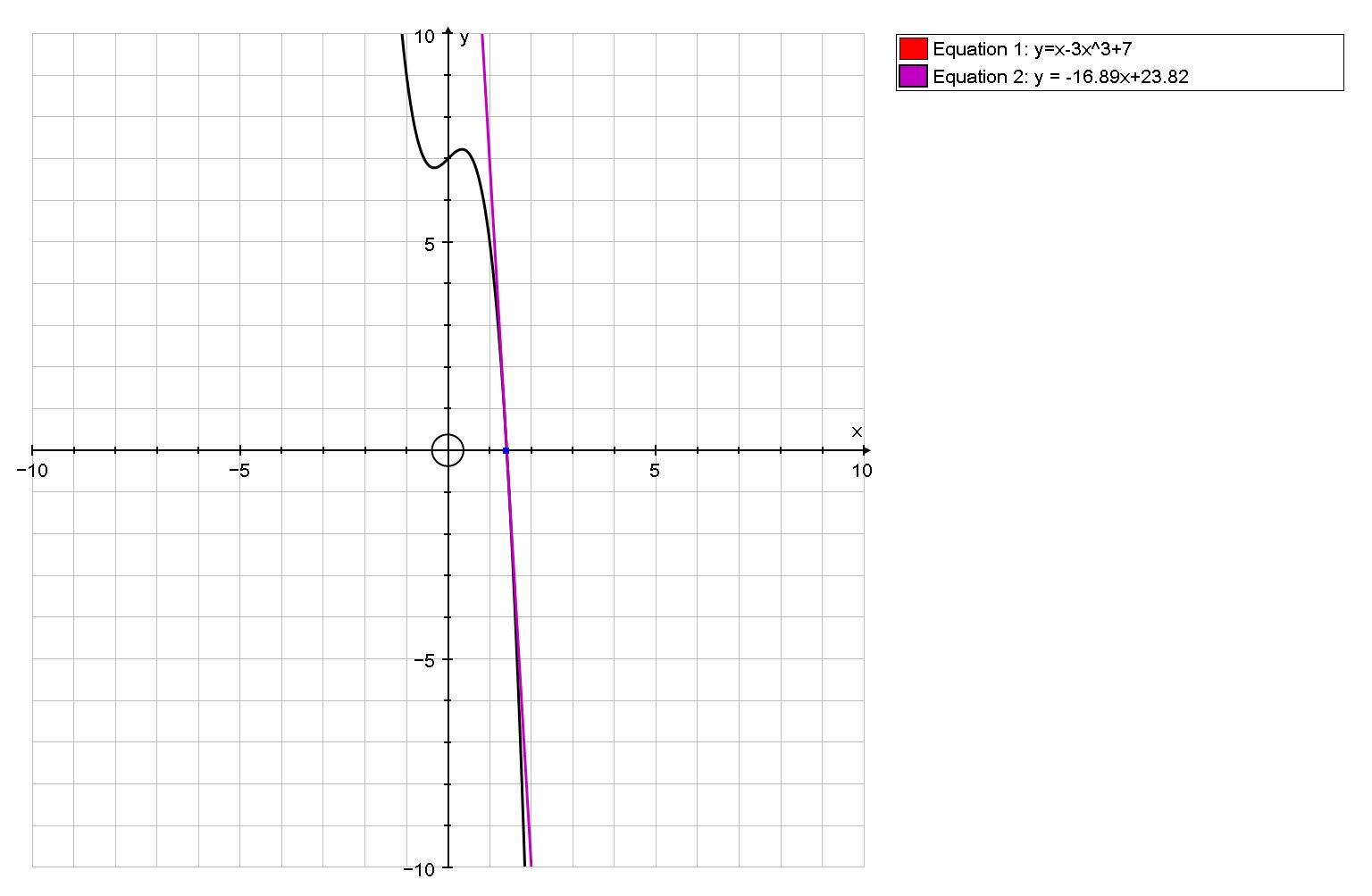
What is the equation of the tangent lines of #f(x) =x-3x^3+7# at # f(x)=0#?

Question

1244 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-03T20:46:25

# y = -16.89x+23.82 # correct to 2dp

The hardest issue with this question is finding the root #x# such that #f(x)=0#. Using Newton-Rhapson I have identified this root to be #1.41# to 2dp

enter image source here

The gradient of the tangent to a function at any particular point is given by the derivative of the function at that point.

Differentiating #f(x)=x-3x^3+7# we get:

# f'(x)=1-9x^2 #

When #f(x)=0 => x =1.41 (2dp)# (N-R)
# :. f'(x) = -16.89340631 ...= -16.89 # (2dp)

So the tangent we seek passes through #(1.41, 0)# and has slope #-16.89#, so using #y-y_1=m(x-x_1)# the equation is;

# y - 0 = -16.89(x-1.41) #
# :. y = -16.89x+23.82 #

We can verify this is correct by the following graph:
enter image source here