How do you use Newton's method to find the two real solutions of the equation #x^4-x^3-3x^2-x+1=0#?
1 Answer
The roots of the equation
Explanation:
First let us look at the graphs (not strictly needed but it gives s insight into the problem):
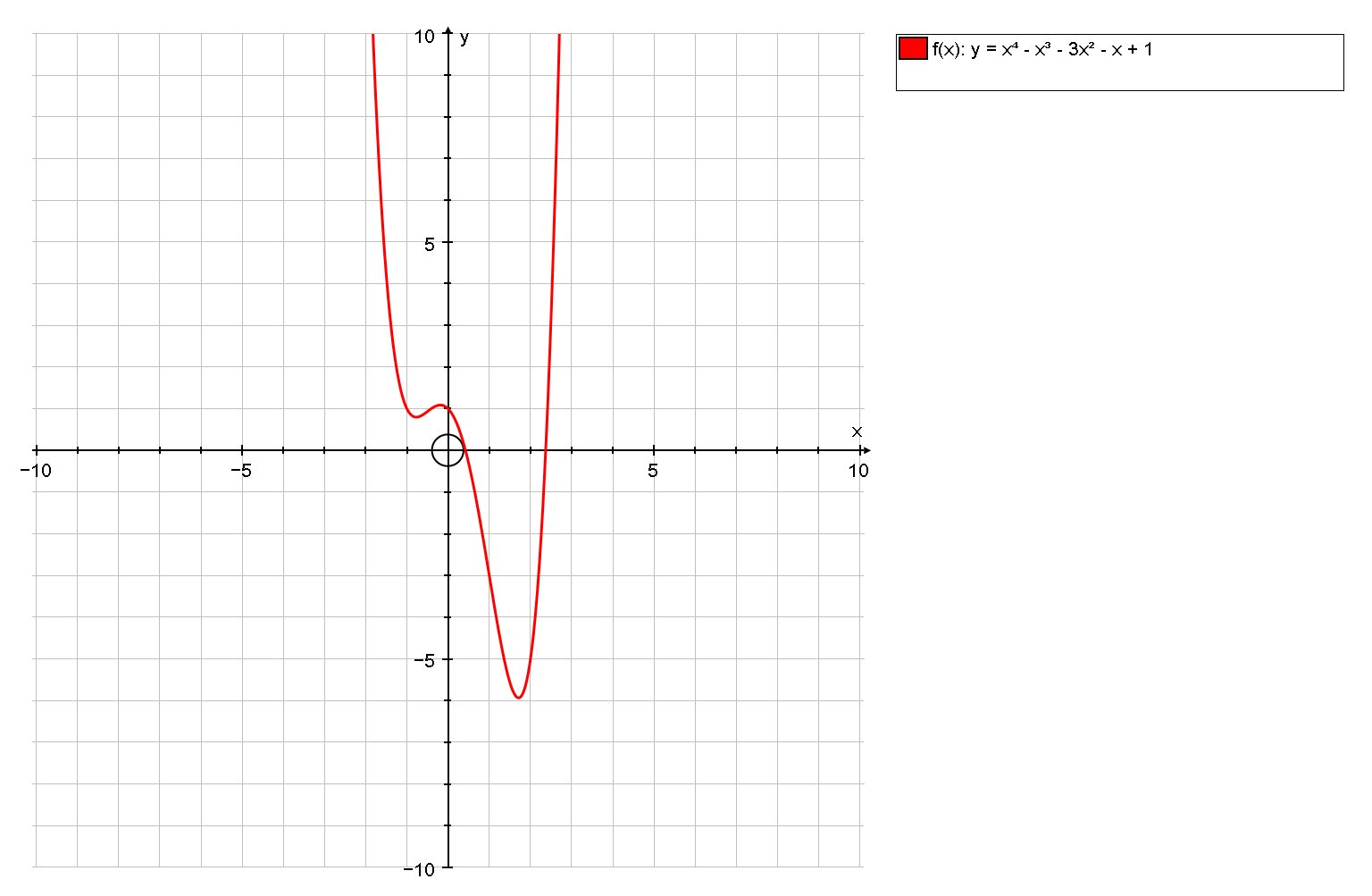
We can see there are two solutions. There is one solution in the interval
Let
#\ \ f(x) = x^4-x^3-3x^2-x+1 => #
# f'(x) = 4x^3-3x^2-6x-1 #
and we will need to apply the Newton-Rhapson method twice to find both roots. We use the following iterative sequence
To find the first root (arbitrarily) choose
Then using excel (working to 6dp) we can tabulate the iterations as follows:

To find the second root (arbitrarily) choose

We would need to vary
And so we conclude that the roots of the equation
#x^4-x^3-3x^2-x+1 =0#
are

