Question

If a projectile is shot at a velocity of `5 m/s` and an angle of `pi/4`, how far will the projectile travel before landing?

Answer 1

`2.55 m`

Explanation:

For Physics or Mechanics you should learn the "suvat" equations for motion under constant acceleration:

`{: (v=u+at, " where ", s="displacement "(m)), (s=ut+1/2at^2, , u="initial speed "(ms^-1)), (s=1/2(u+v)t, , v="final speed "(ms^-1)), (v^2=u^2+2as, , a="acceleration "(ms^-2)), (s=vt-1/2at^2, , t="time "(s)) :}`

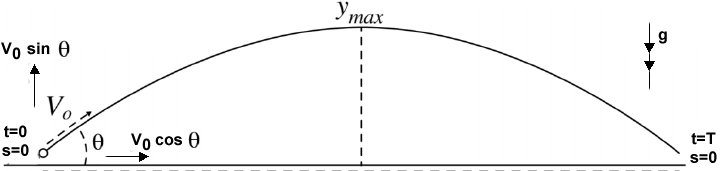
Vertical Motion
Motion under constant acceleration due to gravity, applied vertically upwards

Let the total time that the projectile is in the air be `T`, then then total vertical displacement will be `0`, we would expect two solutions, one will be `t=0`

`{ (s=,0,m),(u=,(5)sin(pi/4)=5/2sqrt(2),ms^-1),(v=,"not required",ms^-1),(a=,-g,ms^-2),(t=,T,s) :}`

So we can calculate `T` using `s=ut+1/2at^2`

`:. 0=5/2sqrt(2)T-1/2gT^2`
`:. 1/2T(5sqrt(2)-gT)=0`
`:. T=0, (5sqrt(2))/g`

Horizontal Motion
Under constant speed (NB we can still use "suvat" equation with a=0). Thje projectile will be in in the air for the same time, `t =T`

`s=(5)cos(pi/4)T`
`:. s=(5sqrt(2))/2T`
`:. s=(5sqrt(2))/2 * (5sqrt(2))/g`
`:. s=25/g`

So using `g=9.8 ms^-2` we have.

`s=25/9.8 = 2.55102...= 2.55 m`