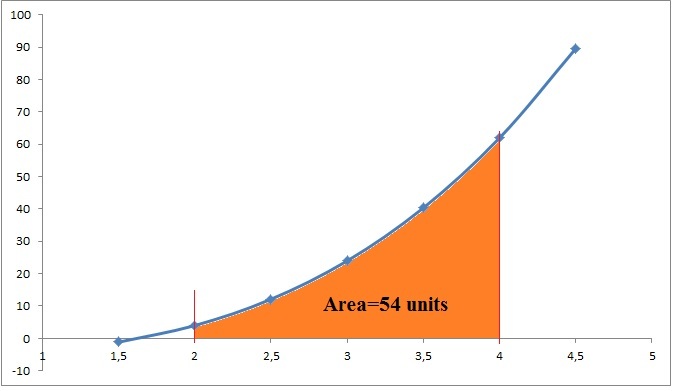
How do you evaluate the definite integral #int (x^3+x-6)dx# from [2,4]?
1 Answer
Dec 9, 2016
I found:
Explanation:
First we can evaluate the integral and then substitute the extremes of integration and subtract the values obtained (Fundamental Theorem of Calculus):
integgrate each one:
For:
we get:
we get:
Finally, subtract the two values:
So:
This value represents the Area below the curve defined by your function between