Question

How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by `y=6sin(5x^2)`, between `0` and `sqrt(pi/5)` revolved about `Ox`?

Answer 1

`2.4pi` (`7.54` 2 dp)

Explanation:

If you imagine an almost infinitesimally thin vertical line of thickness `deltax` between the `x`-axis and the curve at some particular `x`-coordinate it would have an area:

`delta A ~~"width" xx "height" = ydeltax = f(x)deltax`

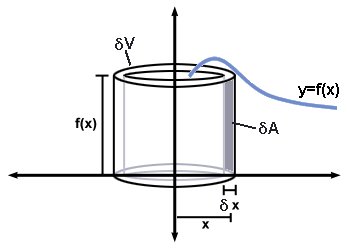
If we then rotated this infinitesimally thin vertical line about `Oy` then we would get an infinitesimally thin cylinder (imagine a cross section through a tin can), then its volume `delta V` would be given by:

`delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax`

If we add up all these infinitesimally thin cylinders then we would get the precise total volume `V` given by:

`V=int_(x=a)^(x=b)2pixf(x) dx`

So for this problem we have:

`\ \ \ \ \ V = int_0^sqrt(pi/5) 2pix(6sin(5x^2)) dx`
`:. V = 12piint_0^sqrt(pi/5) xsin(5x^2) dx`
`:. V = 12pi [-cos(5x^2)/10]_0^sqrt(pi/5)`
`:. V = (-12pi)/10 [cos(5x^2)]_0^sqrt(pi/5)`
`:. V = (-12pi)/10 (cospi-cos0)`
`:. V = (-12pi)/10 (-1-1)`
`:. V = (24pi)/10`
`:. V = 2.4pi` (`~~7.5398...`)