Question

Evaluate? `int_pi^(2pi)theta d theta`

Answer 1

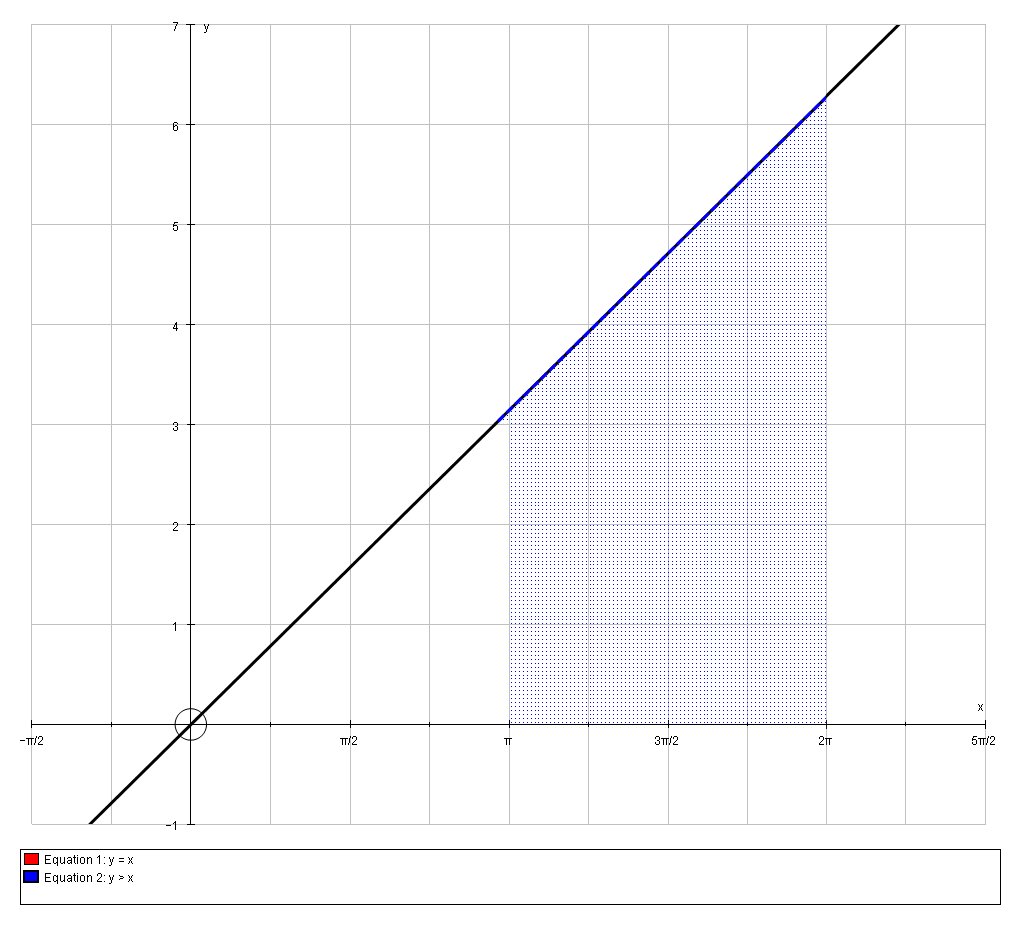
The integral `int_pi^(2pi)theta d theta`, by its very definition represents the area under the graph of the integrand `y=theta` (or `y=x` if you prefer) from `theta=pi` to `theta=2pi` (or `x=pi` to `x=2pi`)

So we have a trapezium of width `pi` and lengths `pi` and `2pi`
So the area of that trapezium is given by:

`A = 1/2(a+b)h`
`\ \ \ = 1/2(pi+2pi)pi`
`\ \ \ = 1/2(3pi)pi`
`\ \ \ = (3pi^2)/2`QED

We can also evaluate the integral using calculus to confirm the result:

`int_pi^(2pi)theta d theta = [1/2theta^2]_pi^(2pi)`
`" " = 1/2[theta^2]_pi^(2pi)`
`" " = 1/2((2pi)^2-(pi)^2)`
`" " = 1/2(4pi^2-pi^2)`
`" " = 1/2(3pi^2)`
`" " = (3pi^2)/2`, reassuringly confirming our result.