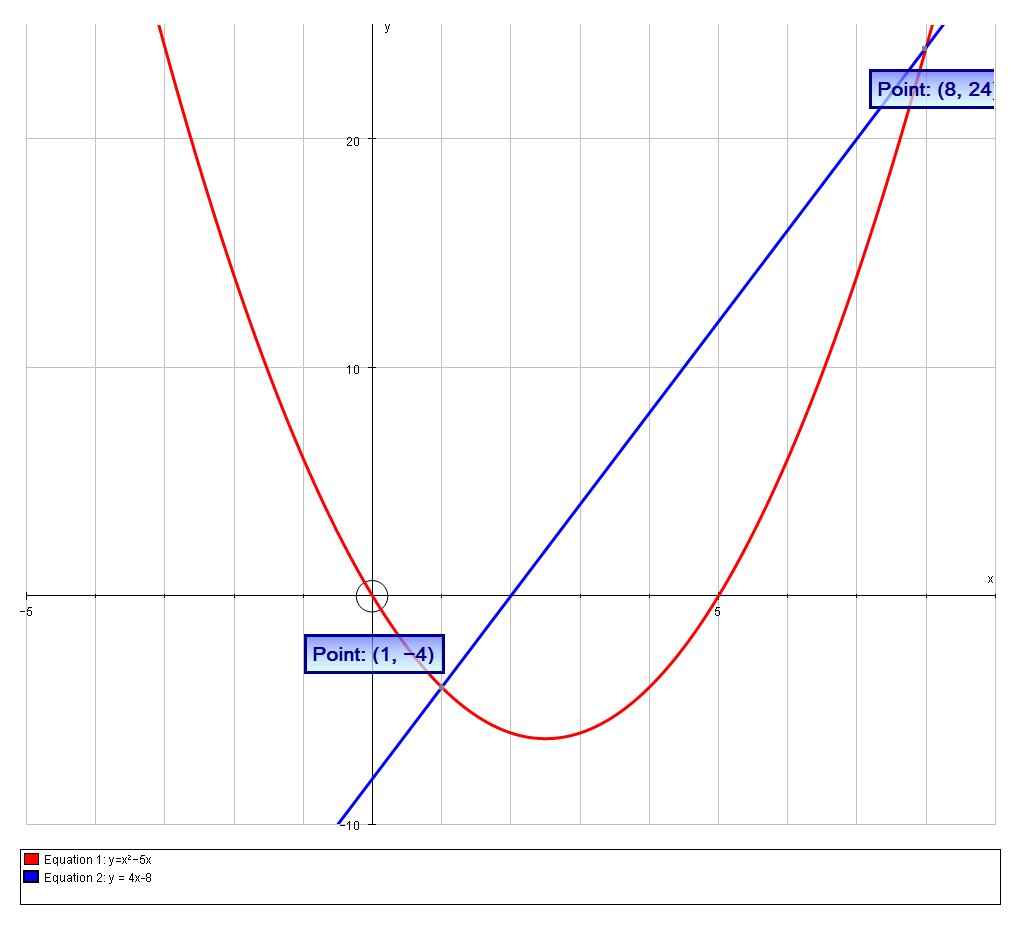
How do you find the equation of the secant line of #f(x)=x^2-5x# through the points [1,8]?
2 Answers
The line will pass through the points
The line will pass through the points
The slope is
The point-slope form of the equation of a line is:
Substitute
Explanation:
We have
When
#x=1 => f(x) = 1-5 = -4#
When#x=8 => f(x) = 64-40 = 24#
So the required secant line passes through the points
We can calculate the slope of the secant line using
#m=(Delta y)/(Delta x) = (24-(-4)) / (8-1) = 28/7 = 4#
So using the factthat the line passes through
# y - (-4)=4(x-1) #
# :. y +4 = 4x-4 #
# :. y = 4x-8 #
NB: We could have equally used the other coordinate
Which we can confirm graphically: