Question

How do you find the equations for the tangent plane to the surface `xy^2+3x-z^2=4` through `(2, 1, -2)`?

Answer 1

`x+y+z=1`

Explanation:

1) rearrange eqn to `" "f(x,y,z)=0`

so:`" "f(x,y,z)=xy^2+3x-z^2-4=0`

2) find normal by calculating`" "gradf(x,y,z), " "at" " (2,1,-2)`

`gradf(x,y,z)=(del/(delx)(xy^2+3x-z^2-4))hati+(del/(dely)(xy^2+3x-z^2-4))hatj+(del/(delz)(xy^2+3x-z^2-4))hatk`

remember when partially differentiating: differentiate with respect to the variable in question, treating the other variables as constant.

`gradf(x,y,z)=(y^2+3)hati+(2xy)hatj-2zhatk`

now evaluate this at `" "(2,1,-2)`

`gradf(2,1,-2)=(1^2+3)hati+(2xx2xx1)hatj-(2 xx-2)hatk`

`gradf(2,1,-2)=4hati+4hatj+4hatk=((4),(4),(4))`

3) the eqn of a plane in vector form is

`vecr * vecn=((x_1),(y_1),(z_1)) * vecn`

where`vecn=((4),(4),(4))` in this case and `"vecr=((x),(y),(z))`

so:

`((x),(y),(z)) * ((4),(4),(4))=((2),(1),(-2)) * ((4),(4),(4))`

`:. 4x+4y+4z=8+4-8`
`:. 4x+4y+4z=4`
`:. x+y+z=1`

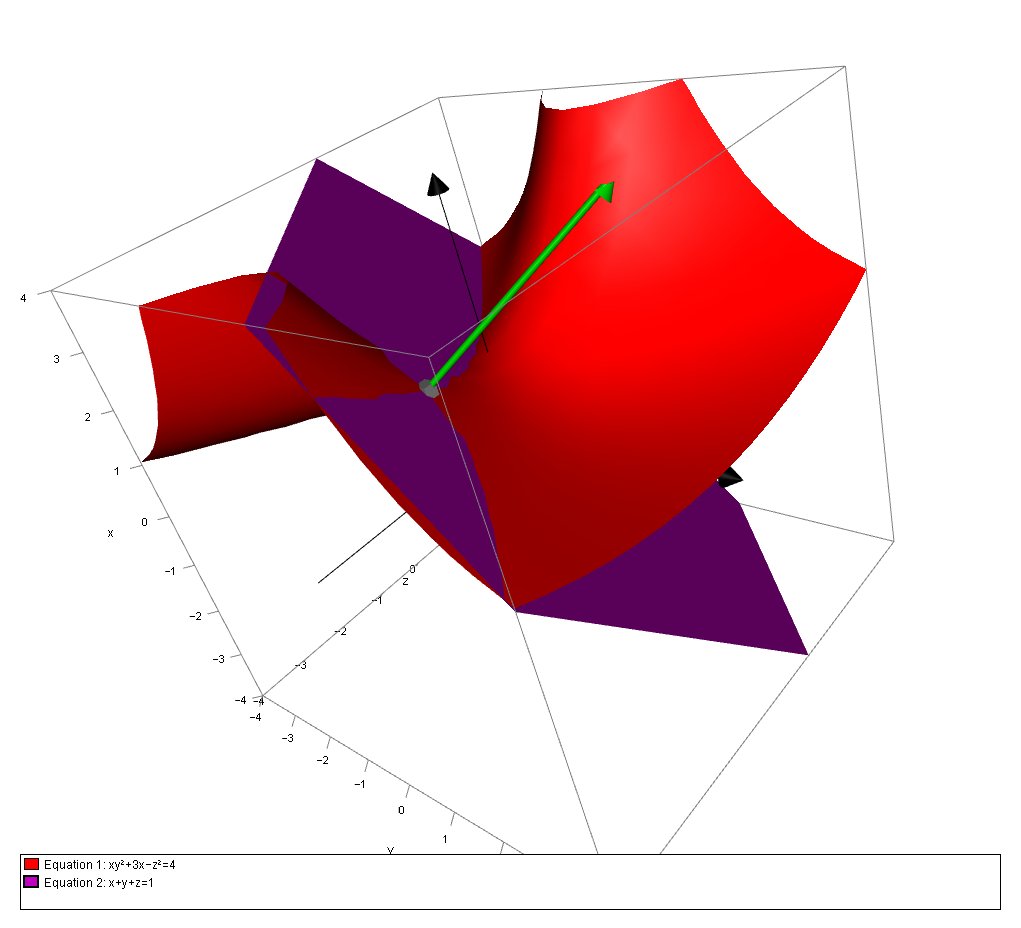
We can confirm this result graphically:

#