How do you find an equation for the line tangent to the circle #x^2+ y^2 =25# at the point (3, -4)?
1 Answer
Explanation:
We could use calculus but first as with all Mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case:
# x^2 + y^2 = 25 #
represents a circle of centre
First verify that
Subs
# => 3^2+y^2=25 = y^2=16 => y=+- 4#
So
# m_N = (Delta y) / (Delta x) = (-4 - 0)/(3 - 0) = -4/3#
Then as the normal is perpendicular to the tangent the product of their gradients is
# m_T = 3/4#
So using the point/slope form
# y-(-4) = 3/4(x-3) #
# :. y+4 \ \ \ = 3/4x-9/4 #
# :. " " y = 3/4x-25/4 #
We can confirm this solution is correct graphically:
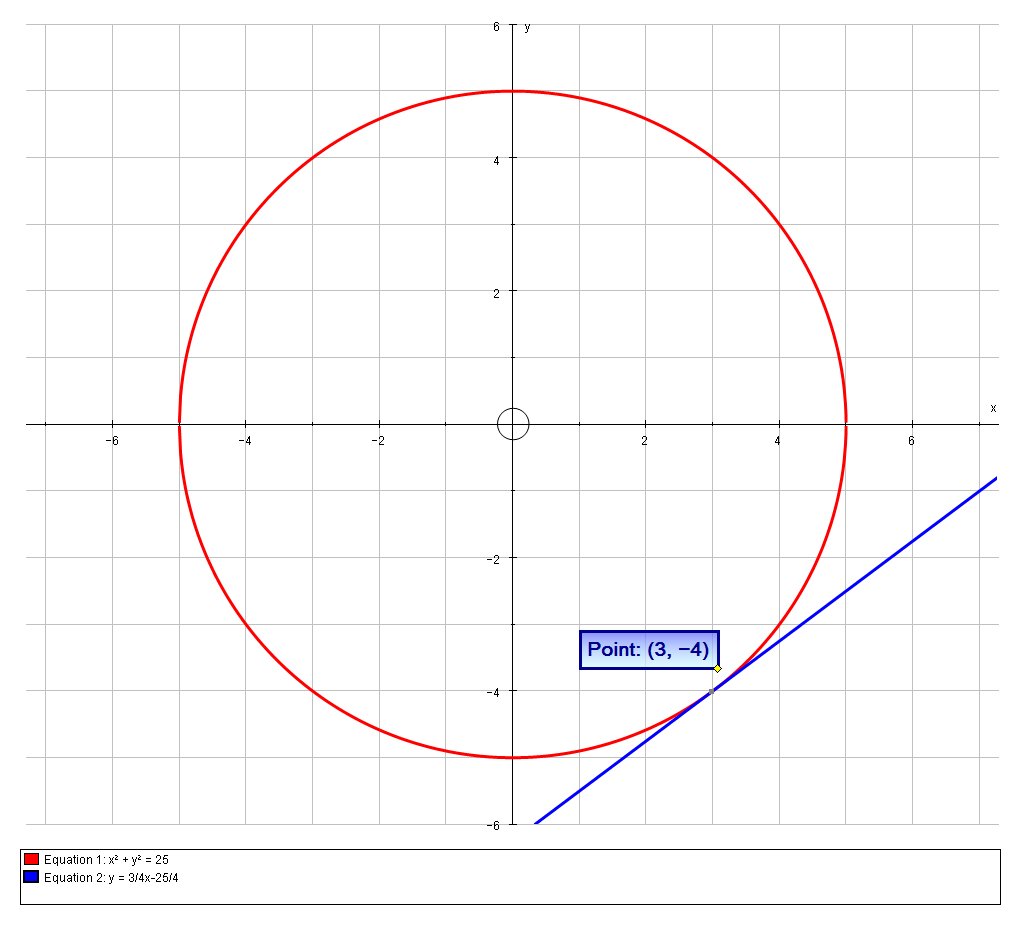
Here is the calculus solution:
If
# 2x+2ydy/dx=0 #
# :. " " dy/dx=-x/y #
When

