Question

A block weighing `14 kg` is on a plane with an incline of `pi/12` and friction coefficient of `1/5`. How much force, if any, is necessary to keep the block from sliding down?

Answer 1

I get `~~9.0N`

Explanation:

We want to know if the forces currently acting on the block will cause it to accelerate (i.e. move down the ramp), and if so, how much force would need to be applied to the block to prevent this. We can test both of these things simultaneously.

A force diagram of the situation:

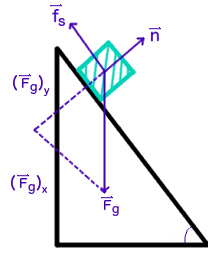
Where `vecf_s` is the force of static friction, `vecn` is the normal force, `vecF_g` is the force of gravity, and `vecF_(gx)` and `vecF_(gy)` are the parallel and perpendicular components of the force of gravity, respectively.

Note that I used the force of static friction, which we want to keep the object from moving. If this is not enough, and the object is accelerating under the given conditions, this is the force of kinetic friction. Whether you call this static or kinetic friction initially will not affect the calculations.

Next, we can put together statements for the parallel and perpendicular forces:

`sumF_x=vecF_(gx)-vecf_s=mveca_x`

`sumF_y=vecn-vecF_(gy)=mcancel(veca_y)=0`

Note that I have defined down the ramp as positive , and so the parallel component of gravity is positive, while the perpendicular component is negative. This can be seen from the force diagram.

Note there is no movement in the vertical direction either way, and so the vertical acceleration is zero, setting the sum of the perpendicular forces equal to zero.

For the object to remain at rest and not slide down the ramp, the net horizontal acceleration must also be zero. We want to know what force, if any, is necessary to make the horizontal acceleration equal zero. We can call this other force `vecF` and rewrite our net parallel force statement:

`sumF_x=vecF_(gx)-vecf_s-vecF=0`

Note that `vecF` is negative. We want it to oppose the motion, which would occur down the ramp (positive).

We can solve for this unknown force:

`vecF=vecF_(gx)-vecf_s`

If no external force is necessary, we should get a value of at most `0`. If not, it indicates that the object would accelerate under the given conditions (only force of gravity, normal force, and force of friction).

• We know the equation for friction: `vecf=muvecn`

• From the sum of forces statement for perpendicular forces, we know that `vecn=vecF_(gy)`

From the force diagram, we can produce equations for the parallel and perpendicular components of the force of gravity. By the magic of geometry, the angle between the vector for the force of gravity (total) and the perpendicular component is the same as the angle of incline of the plane. We see that the parallel component of gravity is opposite the angle, so we will use `sin(theta)` to find it. Similarly, we see that the perpendicular component of gravity is adjacent to the angle, so we will use `cos(theta)` to find it.

We know that the force of gravity is given by `vecF_g=mg`

`vecF_(gx)=mgsin(theta)`

`vecF_(gy)=mgcos(theta)`

Therefore, `vecn=mgcos(theta)`.

Substituting these equations back into the equation we derived for the unknown force:

`vecF=mgsin(theta)-mumgcos(theta)`

`=>vecF=mg(sin(theta)-mucos(theta))`

We can now plug in our known values to solve for `vecF`:

`vecF=(14kg)(9.8m/s^2)(sin(pi/12)-(1/5)cos(pi/12))`

There is no pleasant exact value (not a great angle), but we get `vecF=9.00496831N`.

`vecF~~9.0N`

We can confirm that the object would be accelerating without the added force:

`vecF_x=vecF_(gx)-vecf=mveca_x`

`=>veca_x=(cancel(m)gsin(theta)-mucancel(m)gcos(theta))/cancel(m)`

`=>veca_x=g(sin(theta)-mucos(theta))`

`=>veca_x=(9.8m/s^2)(sin(pi/12)-(1/5)cos(pi/12))`

`=>veca_x~~0.64m/s^2`

`:.` the object would accelerate down the ramp at `0.64m/s^2` under the original conditions.

We can also check our answer:

`sumF_x=vecF_(gx)-vecf-9.00496831N=mveca_x`

`=>veca_x=(mgsin(theta)-mumgcos(theta)-9.00496831N)/m`

`=>veca_x=gsin(theta)-mugcos(theta)-9.00496831N`

`=>veca_x=((14kg)(9.8m/s^2)sin(pi/12)-(1/5)(14)(9.8m/s^2)cos(pi/12)-9.00496831N)/(14kg)`

`=>veca_x=0`

Answer 2

`D=9.00 \ N` (2dp)

Explanation:

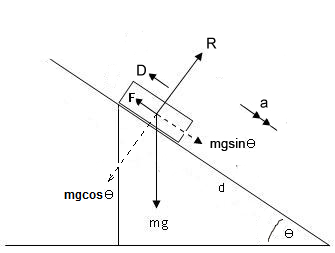
The diagram shows the forces acting on the block, and we have introduced the following variables:

# { (D, "Driving Force to stop block from sliding", N), (F, "Frictional force", N), (R, "Reaction Force from Slope (Newton's 3rd Law)", N) , (m, "Mass of object", 14 \ kg), (a, "acceleration of object down the slope", ms^-2), (theta, "Angle of the slope", pi/12 \ "radians"), (g, "gravitational constant", 9.8 \ ms^-2), (mu, "Static coefficient of friction for block", 1/5) :} #

We would expect the force from gravity to overcome the force of friction and for the block to slide down the plane, However if this is not the case then the maths below will show that this by requiring that `D=0`

Applying Newton's 2nd Law Perpendicular to the plane we get:

`R-mgcostheta = 0`
`:. R=14gcos(pi/12)` .......... [1]

We want the block to be in equilibrium with the force `D` sufficient to stop the block from sliding, so we require no downwards acceleration `=>a=0`, Applying Newtons's 2nd Law Parallel to the plane downwards we get:

`mgsin theta -F -D = 0`
`:. 14gsin(pi/12) - F - D = 0` .......... [2]

If the block is just about to slip we have limiting friction so:

`\ \ \ \ \ F=muR`
`:. F=1/5 14gcos(pi/12)` (from [1])

Substituting back into [2] we get:

`14gsin(pi/12) - 1/5 14gcos(pi/12) - D = 0`
`D= 14gsin(pi/12) - 14/5gcos(pi/12)`

and taking `9=9.8` we get:

`\ \ \ \ \ D=9.004968 ... N`
`:. D=9.00 \ N` (2dp)