A block weighing #8 kg# is on a plane with an incline of #pi/4# and friction coefficient of #2#. How much force, if any, is necessary to keep the block from sliding down?
1 Answer
Explanation:
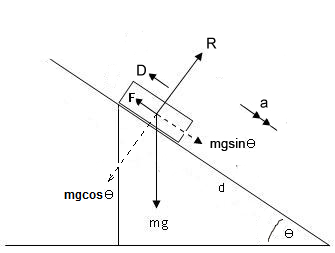
The diagram shows the forces acting on the block, and we have introduced the following variables:
We would expect the force from gravity to overcome the force of friction and for the block to slide down the plane, However if this is not the case then the maths below will show that this by requiring that
Applying Newton's 2nd Law Perpendicular to the plane we get:
#R-mgcostheta = 0#
# :. R=8gcos(pi/4) # .......... [1]
We want the block to be in equilibrium with the force
#mgsin theta -F -D = 0 #
# :. 8gsin(pi/4) - F - D = 0 # .......... [2]
If the block is just about to slip we have limiting friction so:
# \ \ \ \ \ F=muR#
# :. F=2*8gcos(pi/4) # (from [1])
# :. F=16gcos(pi/4) # (from [1])
Substituting back into [2] we get:
# 8gsin(pi/4) - 16gcos(pi/4) - D = 0 #
# D= 8gsin(pi/4) - 16gcos(pi/4) #
and taking
# \ \ \ \ \ D=-55.43717 ... N#
#:. D=-55.44 \ N# (2dp)
Because

