What is the arclength of #(t,t-1)# on #t in [-7,1]#?
1 Answer
Jan 5, 2017
Explanation:
The Arc Length for a Parametric Curve is given by
# L=int_alpha^beta sqrt((dx/dt)^2+(dy/dt)^2) \ dt #
So in this problem we have
# x=t => dx/dt=1 #
# y= t-1 => dy/dt = 1#
So the Arc Length is;
# L=int_-7^1 sqrt((1)^2+(1)^2) \ dt #
# \ \ \= sqrt(2) \ int_-7^1 \ dt #
# \ \ \= sqrt(2) \ [t color(white)int]_-7^1 \ dt #
# \ \ \= sqrt(2) \ {(1)-(-7)} #
# \ \ \= 8sqrt(2) #
Additionally, If we look at the actual graph of the parametric curve:
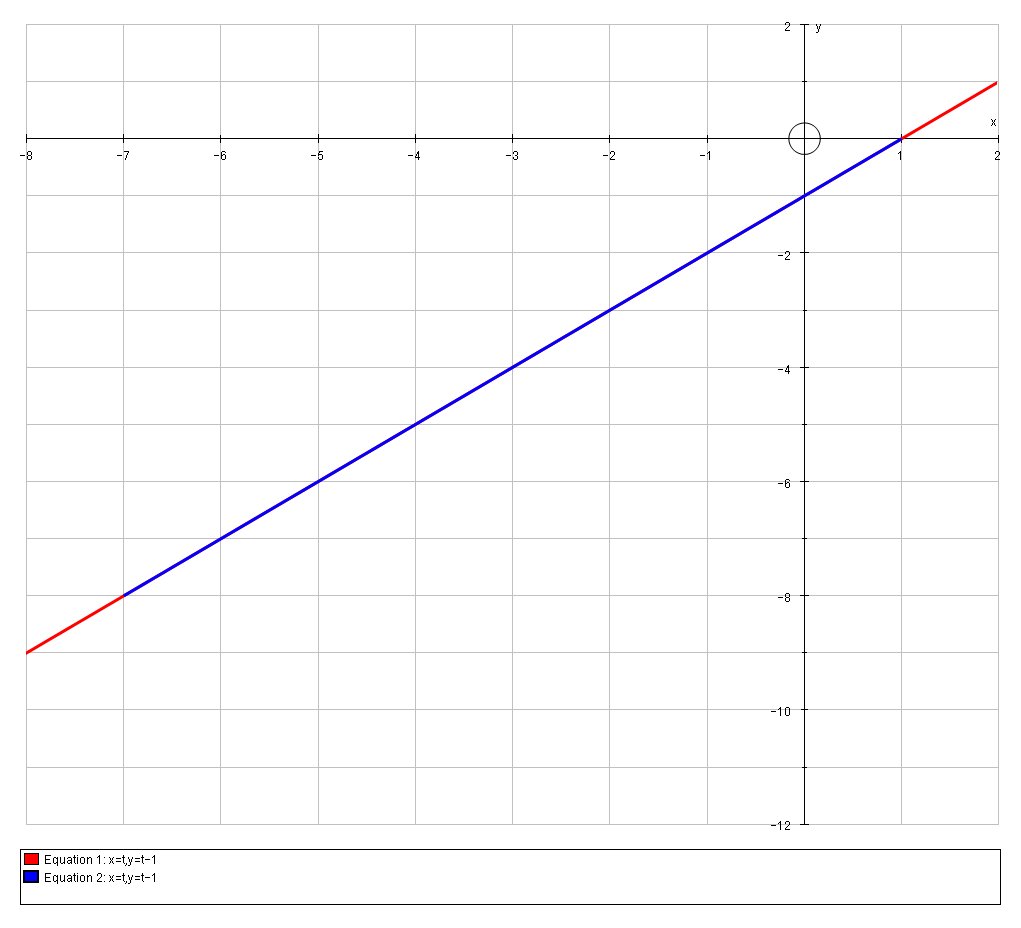
we can see that the equations represent a straight line, so in fact we can easily calculate the are length (coloured blue) from a triangle using Pythagoras:
#L=sqrt((1-(-7))^2 + (0-8)^2) #
# \ \ \=sqrt(8^2+8^2) #
# \ \ \=sqrt(64+64) #
# \ \ \=sqrt(128) #
# \ \ \=8sqrt(2) # , as above
So, Maths Works!

