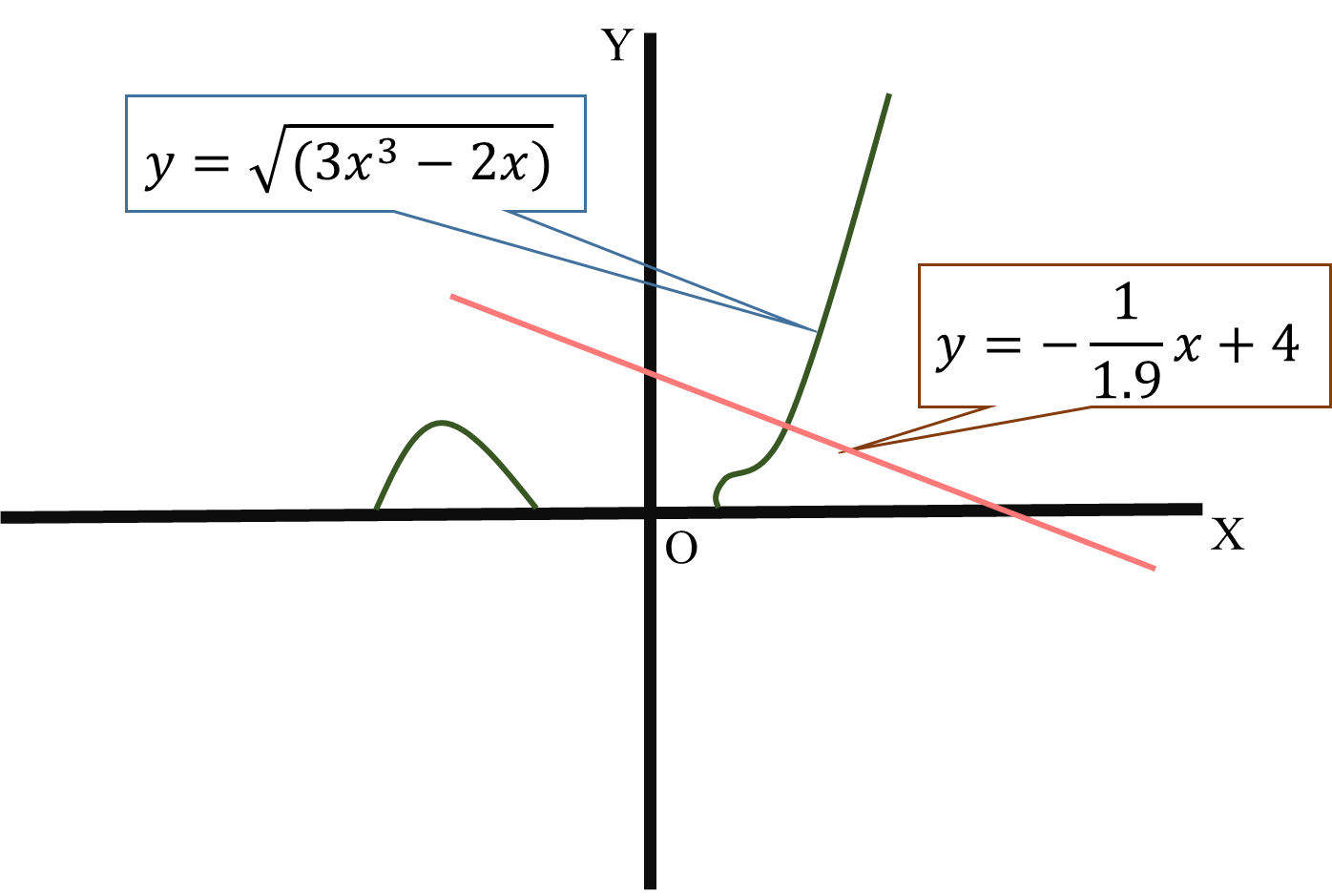
What is the equation of the line normal to #f(x)= sqrt(3x^3-2x) # at #x=2#?

Question

1385 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-07T05:39:22

#y=-1/1.9x+4#

Given -

#y=sqrt(3x^3-2x)#

It slope at any point is given by its first derivative.

#dy/dx=(9x^2-2)/(2* sqrt(3x^3-2x)#

At #x=2# The slope is -

#dy/dx=(9*2^2-2)/(2 * sqrt(3*2^3-2*2))#

#dy/dx=(36-2)/(2*sqrt(24-4))#

#dy/dx=34/(2*sqrt20))#
#dy/dx=34/(2*4.5)#
#dy/dx=34/9=3.8#
#m_1=3.8#

At #x=2# the value of the function is

#y=sqrt(3*2^3-2*2)#
#y=sqrt(24-4)=sqrt 20=4.5#

The normal is passing through the point #(2, 4.5)#

The slope of the normal #m_2=(-1)/m_1=(-1)/3.8#

To find the equation of the normal -

#y=mx+c#
#mx+c=y#
#(-1/3.8)(2)+c=4.5#
#-2/3.8+c=4.5#
#-1/1.9+c=4.5#
#c=4.5-1/1.9=(8.6-1)/1.9=4#
The equation is -
#y=-1/1.9x+4#

enter image source here