Question

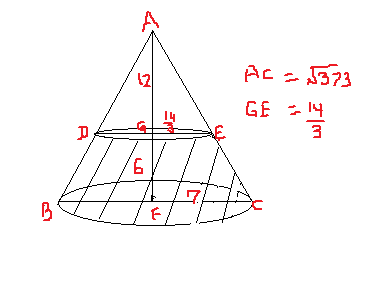
A cone has a height of `18 cm` and its base has a radius of `7 cm`. If the cone is horizontally cut into two segments `6 cm` from the base, what would the surface area of the bottom segment be?

Answer 1

`(637/9 pi +(35sqrt373)/9 pi)` `cm^2`

Explanation:

Since height of cone is 18 and radius of base is 7, its slant height would be `sqrt (18^2 +7^2) = sqrt 373` cms

Area of the slant surface of the cone would be =`pi (7)sqrt373`= `7pi sqrt373` `cm^2.`

Now the cone is horizontally cut 6 cms from the base. it would form a smaller cone of vertical height 12 cms, as shown in the figure below. To find out the radius and slant height of the smaller cone, compare the side ratios of similar triangles AFC and AGE

`(AG)/(AF) = (GE)/(FC)= (AE)/(AC)`

`12/18=(GE)/7= (AE)/sqrt373`, which gives `GE=14/3, AE=(2sqrt373)/3`

Slant surface area of the smaller cone would, thus, be `pi (14/3)(2sqrt373)/3 = pi (28sqrt373)/9` `cm^2`

The bottom segment has been shown as a shaded portion in the figure. Its slant surface area would thus be `(7pisqrt373-pi(28sqrt373)/9)` `cm^2`

To get the total surface area of the bottom segment, area of its top and bottom plane surfaces need to added to the slant surface area.

Area of the top plane surface, which is a circle of radius `14/3`, would be `pi (14/3)^2= pi 196/9` `cm^2`

Area of bottom plane surface, which is a circle of radius 7 would be `49 pi`

Thus the total surface area of bottom segment would be `49 pi +196/9 pi +7 pisqrt373- pi(28sqrt373)/9`

= `(637/9 pi +(35sqrt373)/9 pi)` `cm^2`