If two people pull on either side of the rope with a force of 65N, why is the tension in the rope 65N?
1 Answer
Apply Newton's third law. See below.
Explanation:
The rope experiences the same pulling force on both sides, and therefore it is in a state of static equilibrium (i.e. it is at rest consequently has a net force of zero).
A force diagram:
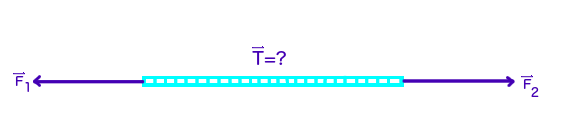
Where
#vecF_1# and#vecF_2# are the pulling forces on the rope and#vecT# is the tension force.#R# will represent the rope later.
Here we consider Newton's third law.
Newton's third law states that every force occurs as a member of an action/reaction pair of forces. You may know it as the familiar phrase, "every action has an equal and opposite reaction." Most importantly, two members of an action/reaction pair are equal in magnitude but opposite in direction.
#vecF_(A on B)=-vecF_(B on A)#
In this situation, each person pulls on the rope with
#vecF_(1 on R)=65N# and#vecF_(2 on R)=65N# .This tells us that the pulling force exerted by each person on the rope is
#65N# , and consequently by NIII, the rope exerts an equal but opposite tension force of#65N# on each person.
This is an action reaction pair. Therefore:
#vecF_(R on 2)=vecF_(2 on R)=vecF_(1 on R)=vecF_(R on 1)=65N#
The tension force in the rope, given by

