A parabola #y=x^2# is parametrised by #x=t# and #y=t^2#. A point P lies on the normal to the parabola at #A(t,t^2)#, and AP is 1 unit in length. Find the equation of the loci of the point #P# as #A# moves?
2 Answers
#P = P(t -2tsqrt(1/(4t^2+1)), t^2 +sqrt(1/(4t^2+1))) #
So the parametric equations of P are:
# P_x(t) = t -2tsqrt(1/(4t^2+1)) #
# p_y(t) = t^2 +sqrt(1/(4t^2+1)) #
Explanation:
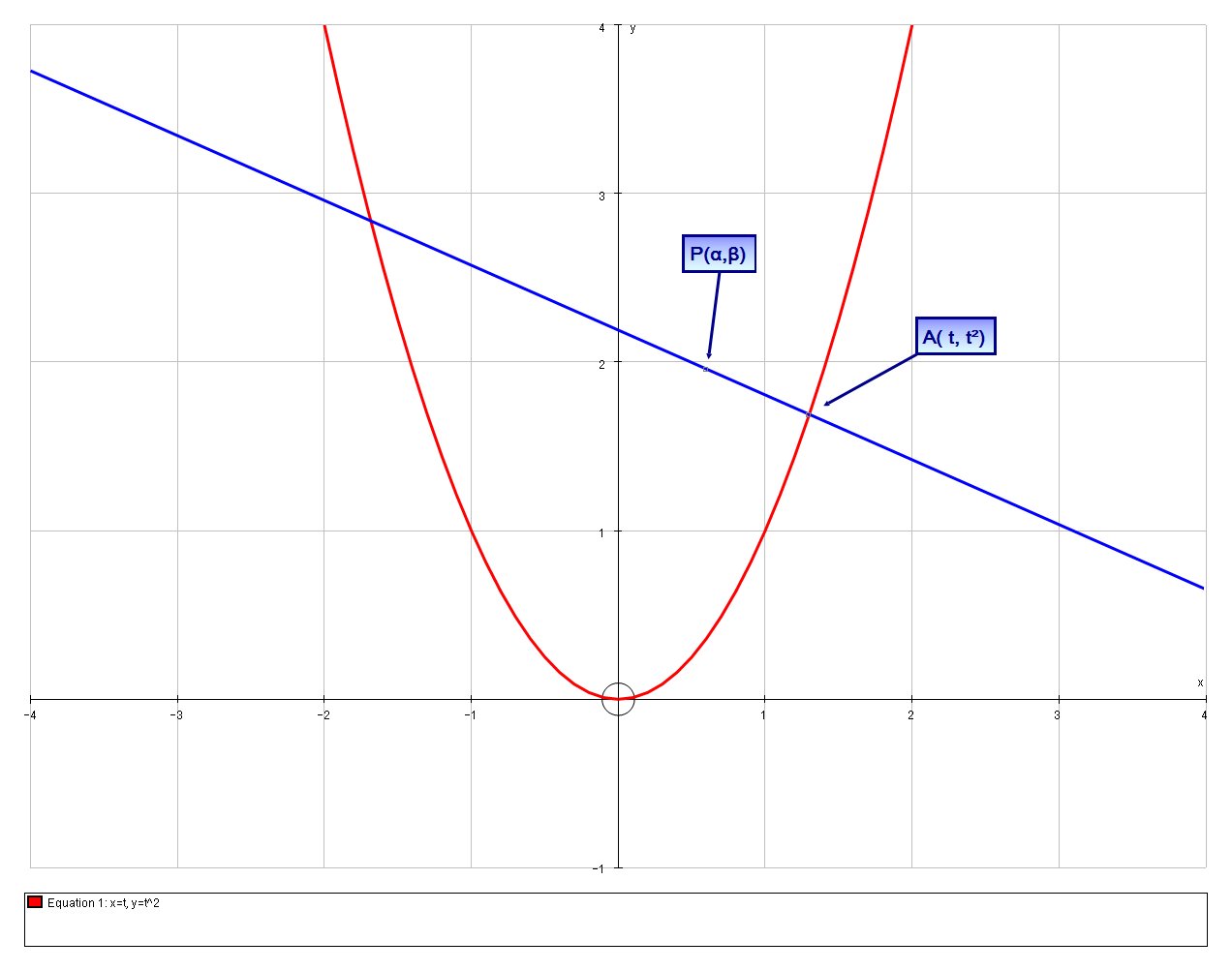
Our parabola
Differentiating wrt
#dy/dx=2x = 2t #
So the gradient of the tangent at
We can now form the equation of the normal
# y-t^2=-1/(2t)(x-t) #
# :. 2ty-2t^3=-(x-t) #
# :. 2ty-2t^3=+t-x #
# :. 2tbeta-2t^3 = t -alpha#
And we are also told that
# (t-alpha)^2+(t^2-beta)^2=1^2 #
We can combine these equations to eliminate
# (2tbeta-2t^3)^2+(t^2-beta)^2=1 #
# :. 4t^2beta^2-8t^4beta+4t^6 + t^4-2t^2beta+beta^2 = 1 #
# :. (4t^2+1)beta^2-2t^2(4t^2+1)beta +t^4(4t^2+1)=1 #
# :. beta^2-2t^2beta +t^4=1/(4t^2+1) #
# :. beta^2-2t^2beta +t^4-1/(4t^2+1) =0#
We can solve this quadratic in
# (beta-t^2)^2-t^4 +t^4-1/(4t^2+1) =0#
# :. (beta-t^2)^2 = 1/(4t^2+1)#
# :. beta-t^2 = +-sqrt(1/(4t^2+1))#
# :. beta = t^2 +-sqrt(1/(4t^2+1))#
We have found two solutions because there is one point
Now from before we have:
#2tbeta-2t^3 = t -alpha# :
# :. alpha = t -2tbeta+2t^3 #
Substituting our valu of
# alpha = t -2t(t^2 +sqrt(1/(4t^2+1)))+2t^3#
# alpha = t -2t^3 -2tsqrt(1/(4t^2+1))+2t^3#
# alpha = t -2tsqrt(1/(4t^2+1))#
And so the general coordinates of
#P = P(t -2tsqrt(1/(4t^2+1)), t^2 +sqrt(1/(4t^2+1))) #
So the parametric equations of P are:
# P_x(t) = t -2tsqrt(1/(4t^2+1)) #
# p_y(t) = t^2 +sqrt(1/(4t^2+1)) #
The loci traced out by
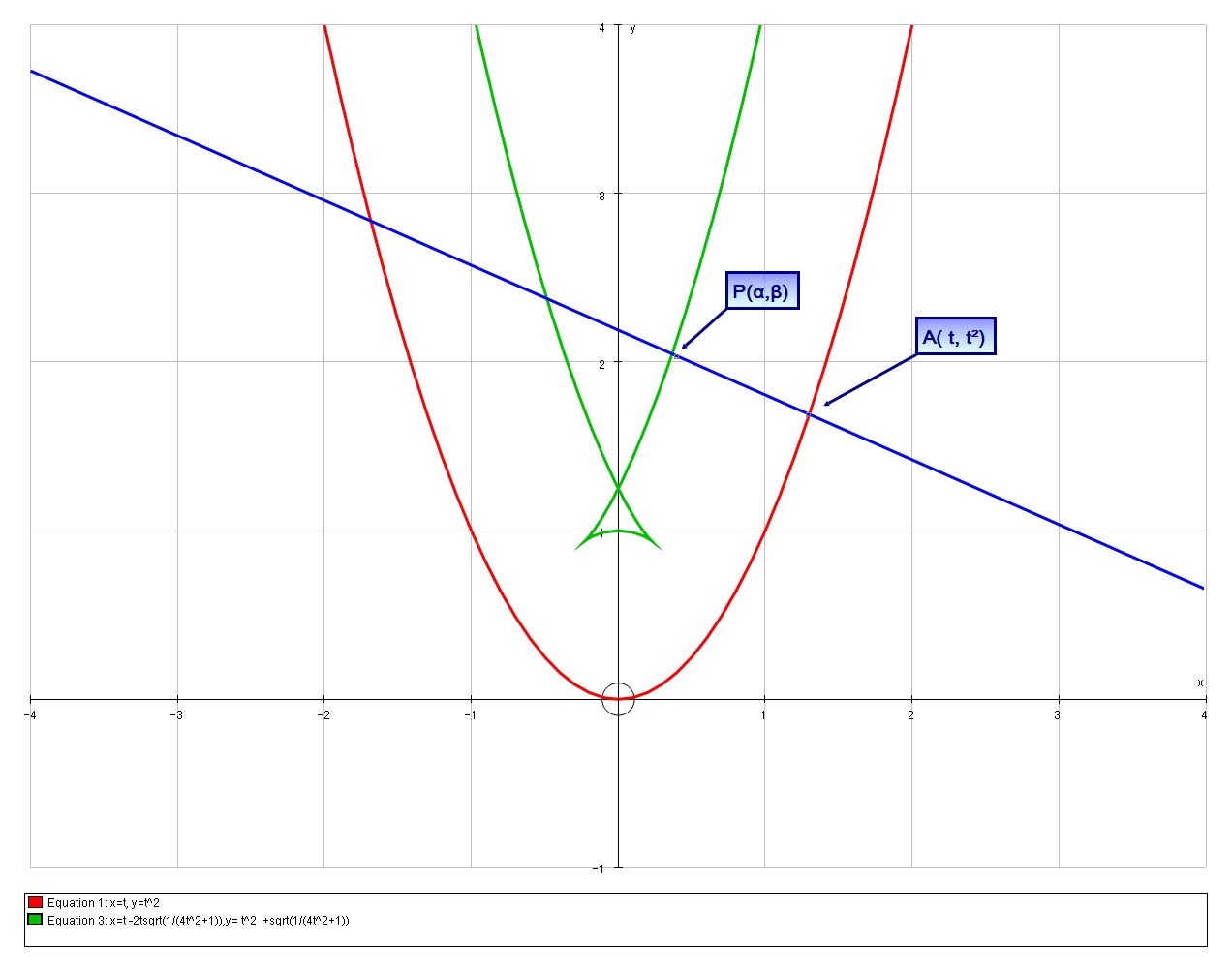
Explanation:
Given
but


