Question

A triangle has corners at `(1 ,2 )`, `(9 ,6 )`, and `(4 ,5 )`. How far is the triangle's centroid from the origin?

Answer 1

`"the centroid of triangle located at :"color(red)(Centroid(4.67,4.33)`
`"length from origin is : "6.37" units"`

Explanation:

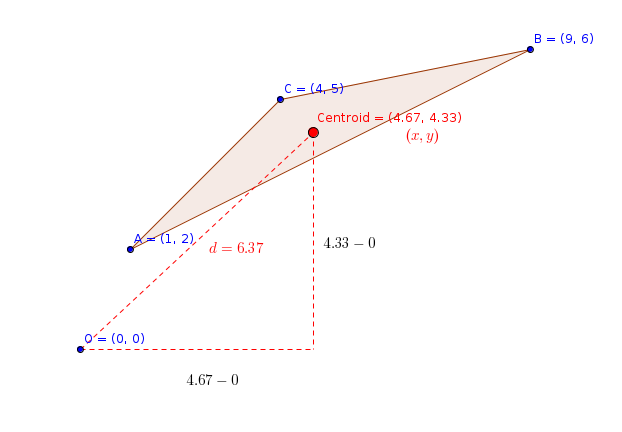
`"Strategy :"`
`diamond " find the centroid of triangle"`coordinates(x,y)
`diamond" find length between origin and centroid"`

`"The coordinates of Centroid "color(red)( Centroid(x,y))" can be calculated using :"`

`x=(x_1+x_2+x_3)/3`

`y=(y_1+y_2+y_3)/3`

`x=(1+9+4)/3=14/3=4.67`

`y=(2+6+5)/3=13/3=4.33`

`"The Centroid located :"color(red)(Centroid(4.67,4.33))`
`"............................................................................................"`
`"length between O(0,0) and "color(red)(Centroid(4.67,4.33))`

`d=sqrt((4.33-0)^2+(4.67-0)^2)`

`d=sqrt((4.33)^2+(4.67)^2)`

`d=6.37" units"`