Calculus Question Using Euler's Method?
In this problem we use Euler’s Method to find an approximate numerical
solution to a differential equation. Assume that y is a function of time t
which satisfies: dy/dt = y^1/3, y(0) = 10
1. Starting with y0 = 10, state Euler’s method for computing yk+1 from yk
with step size ∆t.
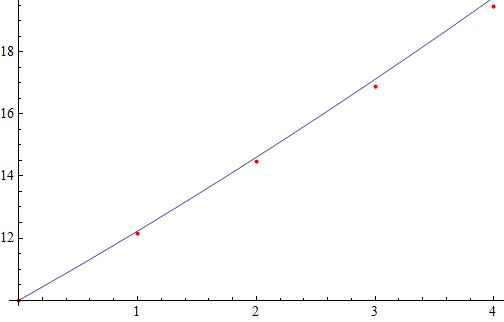
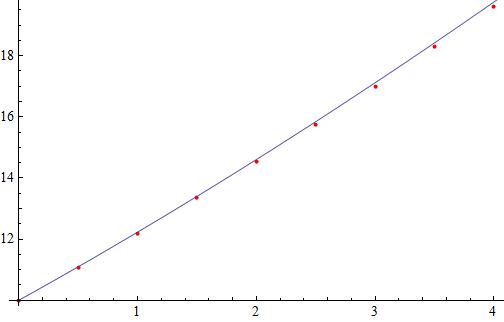
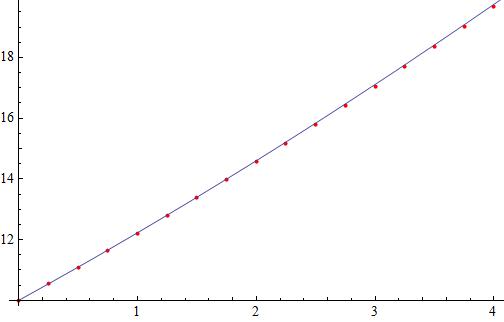
2. Find the values for y1, y2, y3, y4 for step sizes ∆t = 1, 0.5, 0.25 correct to 3 decimal places.
3. State all of the estimates for y(1)
In this problem we use Euler’s Method to find an approximate numerical
solution to a differential equation. Assume that y is a function of time t
which satisfies: dy/dt = y^1/3, y(0) = 10
1. Starting with y0 = 10, state Euler’s method for computing yk+1 from yk
with step size ∆t.
2. Find the values for y1, y2, y3, y4 for step sizes ∆t = 1, 0.5, 0.25 correct to 3 decimal places.
3. State all of the estimates for y(1)
1 Answer
See below.
Explanation:
After making the Euler discretization
Beginning with
we can build the successive approximations for