Question #a76f9
2 Answers
Explanation:
The equations have the form
The tangent lines meet the hyperbola x y = 9 in two coincident
points.
Eliminating y and equating the discriminant of the quadratic
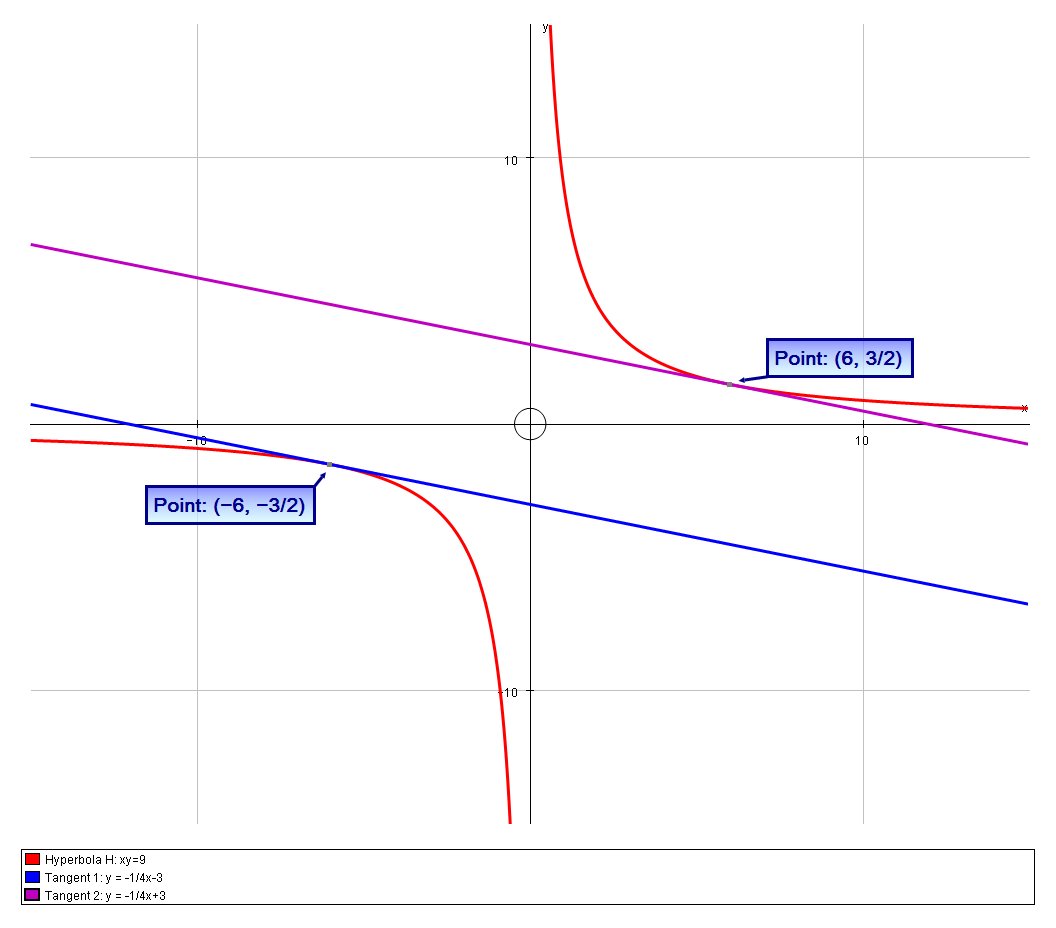
graph{(xy-9)((y+x/4)^2-9)=0 [-40, 40, -20, 20]}
.
The equations of the two tangents that have gradient
#l_1: \ \ \ y = -1/4x-3 #
#l_2: \ \ \ y = -1/4x+3#
Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point.
The equation of the given hyperbola,
# xy = 9 #
Differentiate (implicitly and product rule) the equation of the hyperbola:
# (x)(dy/dx)+(1)(y) = 0 #
# :. dy/dx = -y/x #
A generic point on the hyperbola can be parametrised with a parameter
# x= t => yt=9 => y=9/t #
So a generic point has coordinates
# dy/dx = -y/x = -(9/t)/(t) =-9/t^2 #
At the point where the gradient of the tangent is
# -9/t^2 = -1/4 #
# :. t^2=36#
# :. t=+-6 #
(NB We expected two solutions as there are two tangents!)
Case 1
When
So, the tangent passes through
so using the point/slope form of a straight line
# y-(-3/2)=(-1/4)(x-(-6)) #
# :. y+3/2 = -1/4x-3/2 #
# :. y = -1/4x-3 #
Case 2
When
So, the tangent passes through
so using the point/slope form of a straight line
# y-(3/2)=(-1/4)(x-6) #
# :. y-3/2 = -1/4x+3/2 #
# :. y = -1/4x+3 #
Hence the equations of the two tangents that have gradient
#l_1: \ \ \ y = -1/4x-3 #
#l_2: \ \ \ y = -1/4x+3#
We can verify this graphically: