How do you write an equation of the line tangent to #x^2+y^2-6x-8y=0# at the point (0,0)?
1 Answer
# y = -3/4x #
Explanation:
We have:
# x^2 + y^2 -6x - 8y = 0 #
We can put this into standard form by equating
# x^2 -6x + y^2 - 8y = 0 #
# (x-3)^2 - 3^2 + (y-4)^2 - 4^2 = 0 #
# (x-3)^2 - 9 + (y-4)^2 - 16 = 0 #
# (x-3)^2 + (y-4)^2 = 25 #
# (x-3)^2 + (y-4)^2 = 5^2 #
So the equation is a circle of centre
We can verify by inspection that
The Normal passes through the origin
# m_N =(Delta y) / (Delta x) = (4-0)/(3-0) = 4/3#
The tangent is perpendicular to the Normal so the product of their gradients is
# :. m_T = -1/m_N = -3/4 #
So the tangent passes through the origin
# y-0 = -3/4(x-0) #
# :. y = -3/4x #
We can confirm this graphically;
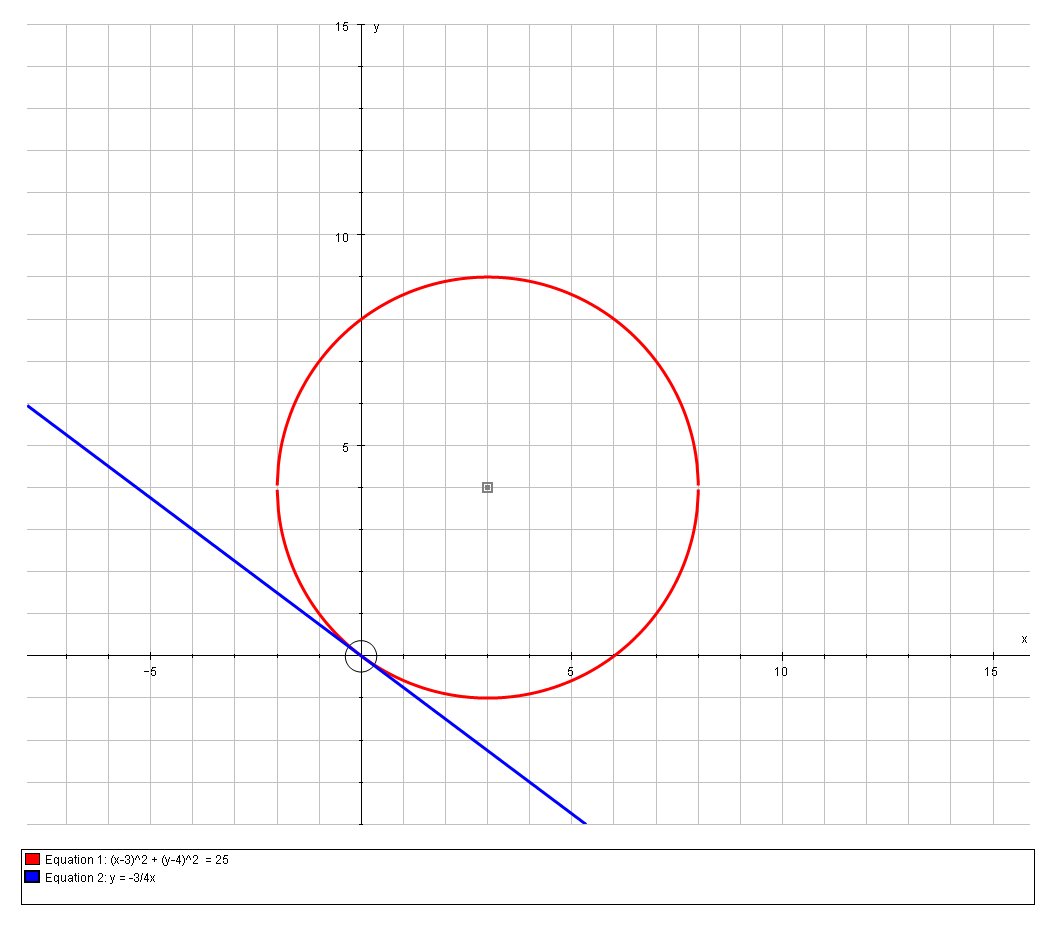
We could also use calculus by differentiating implicitly:
# x^2 + y^2 -6x - 8y = 0 #
# => 2x+2ydy/dx - 6 -8dy/dx = 0 #
At
# 0+0 - 6 -8dy/dx = 0 => dy/dx = -6/8 = -3/4# , as before

