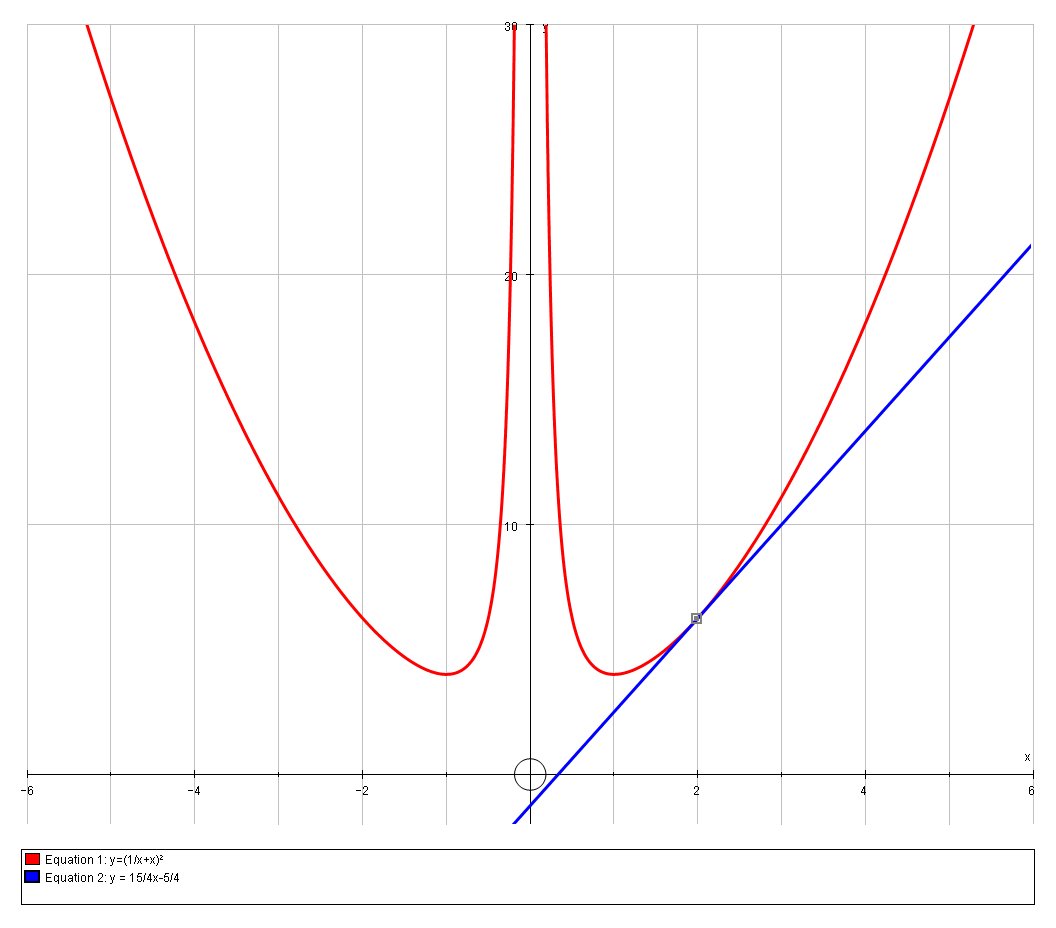
What is the equation of the tangent line of # f(x)=(1/x+x)^2 # at # x=2 #?

Question

1347 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-18T01:42:04

# y = 15/4x-5/4 #

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point.

We have:

# f(x) = (1/x+x)^2 #

Then differentiating wrt #x# (using the chain rule) gives us:

# f'(x) = 2(1/x+x)(-1/x^2+1) #

When #x = 2 => #

# f(2) \ \= (1/2+2)^2 = 25/4 #
# f'(2) = 2(1/2+2)(1-1/4) = 15/4 #

So the tangent passes through #(2,25/4)# and has gradient #15/4# so using the point/slope form #y-y_1=m(x-x_1)# the equation we seek is;

# y-25/4 = 15/4(x-2) #
# :. y = 25/4+15/4x-30/4 #
# :. y = 15/4x-5/4 #

We can confirm this solution is correct graphically:
enter image source here