Question

A force field is described by `<F_x,F_y,F_z> = < xy , 2z-y^2 +x, 2y -zx >`. Is this force field conservative?

Answer 1

The force field is not conservative; `curl(vecF)!=0`.

Explanation:

If `vecF` is a vector (force) field in `RR^3`, then the curl of `vecF` is the vector `curl(vecF)` and is written as `gradxxvecF`. The vector field `vecF` is conservative if and only if `vecF=gradf` for some potential function. If `vecF` is conservative, `curl(vecF)=vec0`. However, this does not mean that a vector field with `curl=vec0` is absolutely conservative; the vector field must also have a potential function to be conservative, but the first prerequisite is that `curl(vecF)=vec0`.

As stated above, the curl is given by the cross product of the gradient of `vecF` (in the form `< P, Q, R >`) and itself.

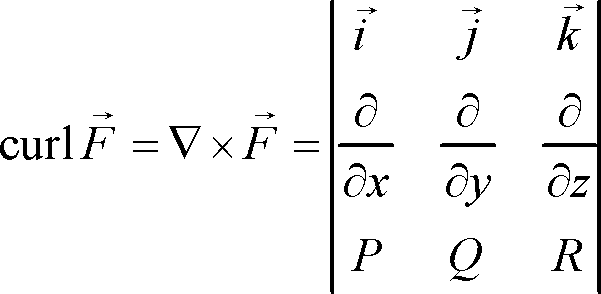
We have `vecF=< xy, 2z-y^2+x, 2y-zx >` where

`P=xy`

`Q=2z-y^2+x`

`R=2y-zx`

The curl of the vector field is then given as:

`abs((veci,vecj,veck),(del/(delx),del/(dely),del/(delz)),(xy,2z-y^2+x,2y-zx))`

We take the cross product as we usually would with vectors, except we'll be taking partial derivatives each time we multiply by a partial differential.

For the `veci` component, we have `del/(dely)(2y-zx)-del/(delz)(2z-y^2+x)`

`=>(2-2)=0`

So far, so good.

For the `vecj` component, we have `del/(delx)(2y-zx)-del/(delz)(xy)`

`=>-(-z-0)=z`

Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is `0` as we treat all other variables as constants.

For the `veck`component, we have `del/(delx)(2z-y^2+x)-del/(dely)(xy)`

`=>(1-x)=1-x`

This gives a final answer of `curl(vecF)=<0,z,1-x> !=vec0`

`:.` Force field is not conservative