Question

How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by `y =x^3`, y= 8 , x= 0 revolved about the x-axis?

Answer 1

Volume `= (768pi)/7 \ \ \ unit^3`

Explanation:

If you imagine an almost infinitesimally thin vertical line of thickness `deltax` between the `x`-axis and the curve at some particular `x`-coordinate it would have an area:

`delta A ~~"width" xx "height" = ydeltax = f(x)deltax`

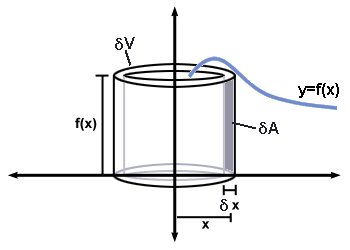
If we then rotated this infinitesimally thin vertical line about `Oy` then we would get an infinitesimally thin cylinder (imagine a cross section through a tin can), then its volume `delta V` would be given by:

`delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax`

If we add up all these infinitesimally thin cylinders then we would get the precise total volume `V` given by:

`V=int_(x=a)^(x=b)2pi \ x \ f(x) \ dx`

Similarly if we rotate about `Ox` instead of `Oy` then we get the volume as:

`V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy`

So for this problem we have:

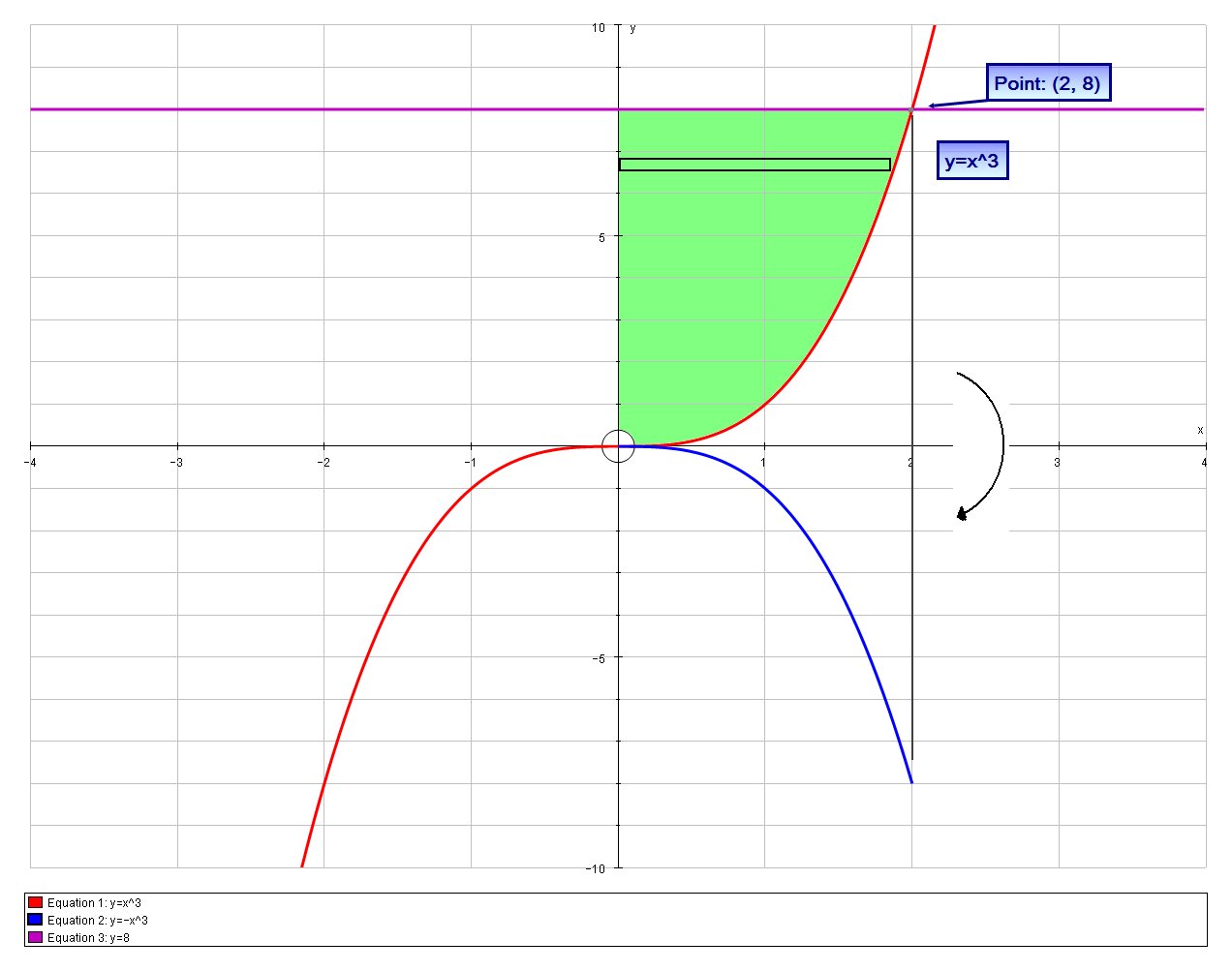
We need the point of intersection for the bounds of integration;

`x \ = 0 => y=0`
`x^3 = 8=>x=2`

And we are integrating wrt `y` so we need `x=g(y)` (ie `f^-1(x)`)

`y=x^3 => x=y^(1/3)`

Then the required volume is given by:

`V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy`
`\ \ \= 2pi int_0^8 \ y*y^(1/3) \ dy`
`\ \ \= 2pi int_0^8 \ y^(4/3) \ dy`
`\ \ \= 2pi [y^(7/3)/(7/3)]_0^8`
`\ \ \= (6pi)/7 [y^(7/3)]_0^8`
`\ \ \= (6pi)/7 (8^(7/3)-0)`
`\ \ \= (6pi)/7 * 128`
`\ \ \= (768pi)/7 \ \ \ unit^3`

Washer Method
We call also use the "washer" method which gives the volume of revolution about `Ox` (this is the non-shaded area under the curve) as:

`V=pi \ int_(x=a)^(x=b) \ (f(x))^2 \ dx`

Which in this problem gives:

`V="(volume bounded by " y=8) - ("volume bounded by " y=x^3)`

Volume bounded by `y=x^3` is:

`V=pi \ int_0^2 \ (x^3)^2 \ dx`
`\ \ \ =pi \ int_0^2 \ x^6 \ dx`
`\ \ \ =pi \ [x^7/7]_0^2`
`\ \ \ =pi \ (128/7 - 0)`
`\ \ \ =(128pi)/7`

The required volume of revolution is then the volume of a cylinder (`pir^2h`) of height `2`, radius `8` minus this result:

`V=(pi)(64)(2) - (128pi)/7`
`\ \ \ =128pi - (128pi)/7`
`\ \ \ =(768pi)/7`, as before

Or if you prefer, we can perform the calculation in a single integral, as:

`V="(volume bounded by " y=8) - ("volume bounded by " y=x^3)`
`\ \ \ =pi \ int_0^2 \ (8)^2 \ dx - pi \ int_0^2 \ (x^3)^2 \ dx`
`\ \ \ =pi \ int_0^2 \ (8)^2 - (x^3)^2 \ dx`
`\ \ \ =pi \ int_0^2 \ 64-x^6 dx`
`\ \ \ =pi \ [64x-x^7/7]_0^2`
`\ \ \ =pi \ (128-128/7 - 0)`
`\ \ \ =(768pi)/7`, as before