Differentiate the following function? y = (8 x)/ (6 - cot x)
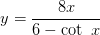
1 Answer
Feb 28, 2017
# dy/dx = 8( (6-cotx - xcsc^2x) ) / (6-cotx)^2#
Explanation:
We apply the Quotient Rule for Differentiation:
# d/dx(u/v) = (v(du)/dx-u(dv)/dx)/v^2 # , or less formally,# " "(u/v)' = (v(du)-u(dv))/v^2 #
I was taught to remember the rule in word; " vdu minus udv all over v squared ". To help with the ordering I was taught to remember the acronym, VDU as in Visual Display Unit.
So with
# :. dy/dx = (v(du)/dx-u(dv)/dx)/v^2 #
# " " = ( (6-cotx)(8) - (8x)(csc^2x) ) / (6-cotx)^2#
# " " = 8( (6-cotx - xcsc^2x) ) / (6-cotx)^2#

