A triangle has corners at #(1 ,3 )#, #(9 ,2 )#, and #(6 ,7 )#. How far is the triangle's centroid from the origin?

Question

930 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-03-02T09:29:51

#"The answer is l=6.67 units"#

#"the triangle A(1,3),B(9,2),C(6,7) is shown in figure below"#

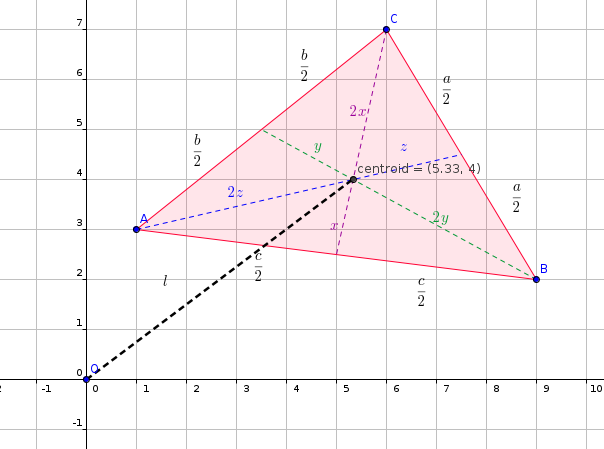
enter image source here

#"The centroid of any triangle can be calculated using the formula below."#

#centroid(x,y)#

#"Centroid of any triangle represents by two values (x,y)"#

#x=(x_A+x_B+x_C)/3#

#y=(y_A+y_B+y_C)/3#

#A(1,3)" "rArr " "x_A=1" , "y_A=3#

#B(9,2)" "rArr" "x_B=9" , "y_B=2#

#C(6,7)" "rArr" "x_C=6" , "y_C=7 #

#x=(1+9+6)/3=16/3=5.33#

#y=(3+2+7)/3=12/3=4#

#centroid(5.33,4)#

#"let distance between origin and centroid be l;"#

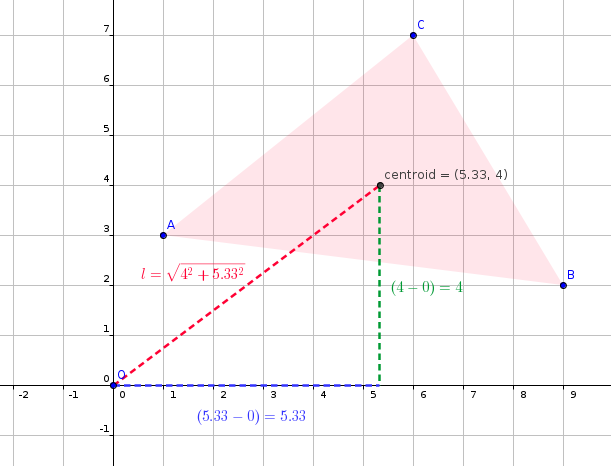
enter image source here

#l=sqrt((y_("centroid")-y_("origin"))^2+(x_("centroid")-x_("origin"))^2)#

#l=sqrt((5.33-0)^2+(4-0)^2)#

#l=sqrt((5.33)^2+4^2)#

#l=sqrt(28.41+16)#

#l=sqrt(44.41)#

#l=6.67#