If #f(x)=x^(1/2)#, #1 <= x <= 4# approximate the area under the curve using ten approximating rectangles of equal widths and left endpoints?
1 Answer
Area
Explanation:
We have:
# f(x) = sqrt(x) #
We want to calculate over the interval
# Deltax = (4-1)/10 = 0.3#
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;
Left Riemann Sum
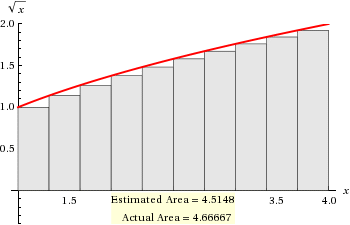
# LRS = sum_("left") f(x)Deltax #
# " " = (0.3) { f(1)+f(1.3) + f(1.6) + ... +f(3.4) + f(3.7) } \ \ \ # (The LHS values)
# " " = 0.3*(1+1.140175425+1.264911064+1.378404875+#
# " " 1.483239697+1.58113883+1.673320053+#
# " " 1.760681686+1.843908891+1.923538406#
# " " = 0.3*15.04931893 #
# " " = 4.514795679 #
Actual Value
For comparison of accuracy:
# Area = int_1^4 \ x^(1/2) \ dx #
# " " = [(x^(3/2))/(3/2)]_1^4 #
# " " = 2/3[x^(3/2)]_1^4 #
# " " = 2/3{(8) - (1)} #
# " " = 14/3 #
# " " ~~ 4.6667 #


