Find the limit ?
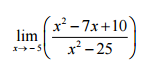
2 Answers
I would say that it tends to
Explanation:
If you use
this tells us that as
Graphically:
graph{(x^2-7x+10)/(x^2-25) [-12.66, 12.65, -6.33, 6.33]}
as you can see at
Explanation:
Use direct substitution:
Thus, the limit does not exist because
Check with a graph:
graph{(x^2-7x+10)/(x^2-25) [-12.66, 12.65, -6.33, 6.33]}
As you can see, at
*Note: We cannot use L'Hospital's rule because


