How to solve this equation where z is a complex number #(2z+2i)^4=z^4#?
2 Answers
Explanation:
or
so we have:
or
Explanation:
We have:
# (2z+2i)^4 = z^4 #
# :. ((2z+2i)^2)^2 - (z^2)^2 = 0#
Which is the difference of two squares; and so we use:
#A^2-B^2-=(A+B)(A-B)#
to give:
# ((2z+2i)^2 - z^2) ((2z+2i)^2 + z^2) = 0#
The first factor is again the difference of two square and using
# ((2z+2i)^2 - z^2) ((2z+2i)^2 - (iz)^2) = 0#
# :. ((2z+2i) - z) ((2z+2i) + z) ((2z+2i) - iz)((2z+2i) + iz) = 0#
# :. (z+2i) (3z+2i) (2z- iz+2i )(2z+ iz+2i ) = 0#
And so we have four solution:
(a)
# z+2i = 0 => z=-2i # (b)
# 3z+2i = 0 => z=-2/3i # (c)
# 2z- iz+2i = 0 => z(2-i)=-2i #
# :. z = (-2i)/(2-i) * (2+i)/(2+i) = (-4i-2i^2)/(4-i^2)=2/5-4/5i# (d)
# 2z+ iz+2i = 0 => z(2+i)=-2i #
# :. z = (-2i)/(2+i) * (2-i)/(2-i) = (-4+2i^2)/(4-i^2)=-2/5-4/5i#
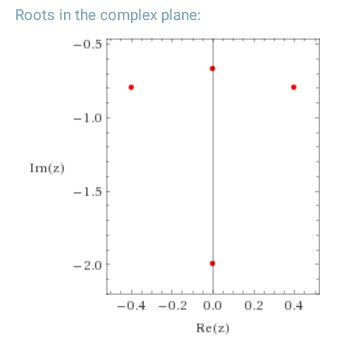
Which we can plot on the Argand diagram: