Question

Find the constraints, make a plot, find the maximum number of attendants, and compute the minimum cost solution for the problem below? Also, show that `4x+3y<=20` and `99x + 104y <= 600` are two of the constraints.

William is a clothing maker, and his sister is getting married. He has agreed to make the suits and dresses for all the pageboys and bridesmaids, as long as he doesn't work more than 100 hours. It takes him 20 hours to make one dress and 15 hours to make one suit. Her sister has a budget of ₤600, and fabric costs ₤8/m. A dress needs 8m of fabric, while a suit needs 3m of fabric. He charges an additional ₤35 to make a dress and an extra ₤80 for making each suit.

Answer 1

Constraints:

`4x+3y <= 20`
`99x+104y<= 600`
`x>= 1`
`y>=1`

See explanation for plot.
Maximum number of attendants: 5.
Minimum cost solution is 1 bridesmaid and 4 pageboys.

Explanation:

To help this make more sense, let's think of `x` as the number of bridesmaid dresses and `y` as the number of pageboy suits. Since the number of dresses equals the number of bridesmaids (and same for the pageboys/suits), the maths are identical. With that said, we need to figure out the restrictions on these variables.

Let's start with the time restriction. We can't go over 100 hours, and if it takes 20 hours to make a dress and 15 hours to make a suit, then we get the following constraint:

`["20 hr"/"dress" times x " dresses"]+["15 hr"/"suit" times y " suits"] <= "100 hours"`

What does this mean? If William plans to make `x` dresses, then he needs to allow for `20x` hours to make them. Similarly, he'll need to allow `15y` hours to make `y` suits. Since these two times cannot total more than the 100 hours William is available, the inequality above simplifies to:

`20x+15y<=100`

which reduces to

`4x+3y <= 20`

which is the first constraint we were asked to show.

What's another "limit" we need to stay under? The cost. William can't spend more than ₤600 on all the outfits. So, how much does it cost to make each outfit?

For a dress, the cost is

`["8m fabric"/"dress" times "₤8"/"1m fabric"]+"₤35 (extra cost)"/"dress"`

`="            ""₤64"/"dress""                 "+"         ""₤35"/"dress"`

`=" ₤99/dress"`

Likewise, for a suit, the cost is

`["3m"/"suit" times "₤8"/"m"]+"₤80"/"suit"" "=" ""₤104/suit"`

So, if he wants to make `x` dresses and `y` suits, the next constraint is

`["₤99"/"dress" times x " dresses"]+["₤104"/"suit" times y " suits"] <= "₤600"`

or

`99x+104y<= 600`

The other two constraints are given to us verbatim in the question: we must have at least 1 bridesmaid (and thus at least 1 dress) and at least 1 pageboy (meaning at least 1 suit). These are written as

`x>= 1" "` and `" "y>=1`.

To plot the region of acceptable values for `x` and `y`, all we do is plot these 4 inequalities (lines) on a single graph, like this:

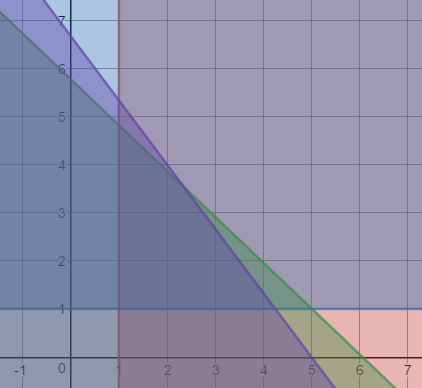
The acceptable region for `x` and `y` to be in simultaneously is the 4-sided "triangle-like" shape—below the diagonal lines, and "above" the perpendicular lines; the points on the gridlines within this shape are the only points we can occupy.

The maximum number of attendants is the largest sum of `x` and `y` (call this `k=x+y`) that lies within our shape. By sight, we can see that `k=5` will be the largest such value, since there are 4 points where `x+y=5` within our shape, but none where `x+y=6`. Thus, the maximum number of attendants is 5.

William's sister pays him for his materials and his time, so her overall cost for each dress is

`"₤99 in materials " + ["₤15"/"hour" times "20 hours"]`
`=₤99+₤300`
`=₤399`

and her overall cost for each suit is

`"₤104 in materials " + ["₤15"/"hour" times "15 hours"]`
`=₤104+₤225`
`=₤329`

So we want to minimize the expression `399x+329y`, where `x+y=5`.

This is easy enough: since the overall cost for a suit is less than that for a dress, we want to minimize the number of dresses we order (to minimize the cost). Thus, the minimum cost solution is `(x,y)=(1,4)`, or 1 bridesmaid dress and 4 pageboy outfits.