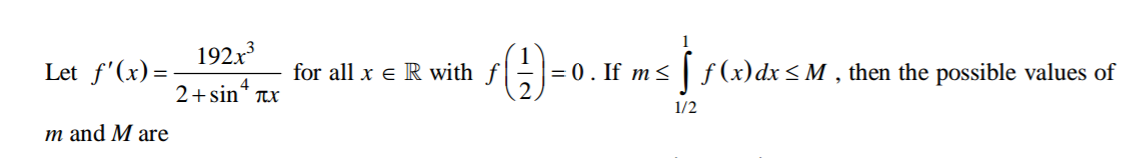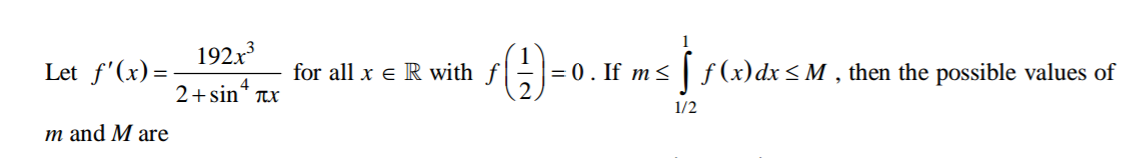#f'(x)# is monotonic increasing for #1/2 le x le 1# and
#f'(1/2)=(192(1/2)^3)/(2+1)=8#
#f'(1)=192/2=96#
then
#f(1/2)+f'(1/2)(x-1/2) le f(x) le f(1/2)+f'(1)(x-1/2)#
but #f(1/2)=0# so
#int_(1/2)^1f'(1/2)(x-1/2)dx le int_(1/2)^1f(x)dx le int_(1/2)^1f'(1)(x-1/2)dx#
or
#8int_(1/2)^1(x-1/2)dx le int_(1/2)^1f(x)dx le 96int_(1/2)^1 (x-1/2)dx#
or finally
#8/8 le int_(1/2)^1f(x)dx le 96/8#
or
#m = 1# and #M = 12#