Question

A block weighing `6 kg` is on a plane with an incline of `(3pi)/8` and friction coefficient of `2/5`. How much force, if any, is necessary to keep the block from sliding down?

Answer 1

The force is `=63.3N`

Explanation:

Let the force be `F`

The frictional force is

`mu_s=F_r/N`

`N=mgcostheta`

`F_r=mu_s*mg costheta`

Resolving in the direction parallel to the plane `↗^+`

The force is

`F=F_r+ mgsintheta`

`F=mu_s mgcostheta+mgsintheta`

`=2/5*6*9.8cos(3/8pi)+6*9.8*sin(3/8pi)`

`=(9+54.3)N`

`=63.3N`

The force is `=63.3N`

Answer 2

`"it is necessary a force 45.38 Newtons"`

Explanation:

`"given data :"`
`m:6 " "kg" mass of block"`
`g=9.81 " "N/(kg)`
`beta=(3pi)/8`
`mu_k=2/5`

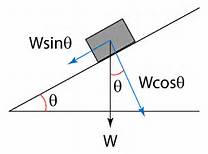
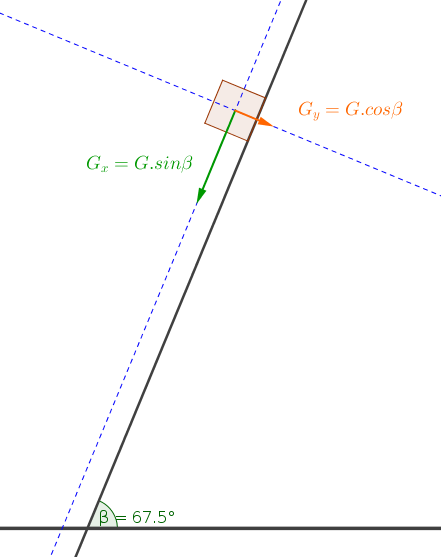
`"The block appears as if it were given on an inclined plane."`
`"Please notice that the weight of of block is perpendicular"`
`"to the ground."`

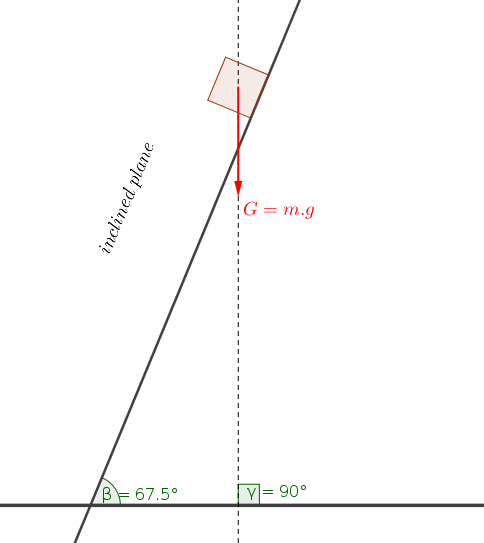
`"You should split the weight of block into two components "`

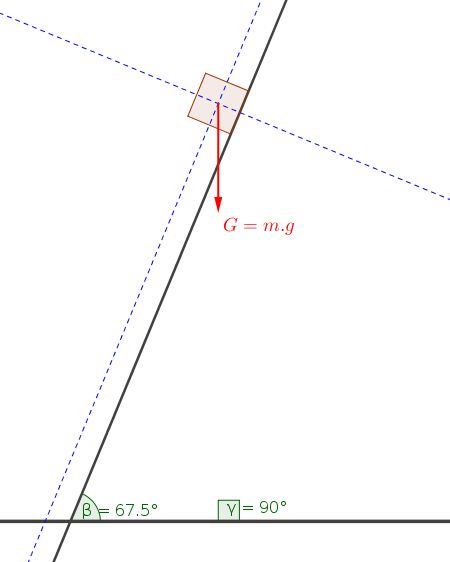
`"The green vector "G_x " is parallel to the inclined plane."`

`"The orange vector "G_y " is perpendicular to the inclined plane."`

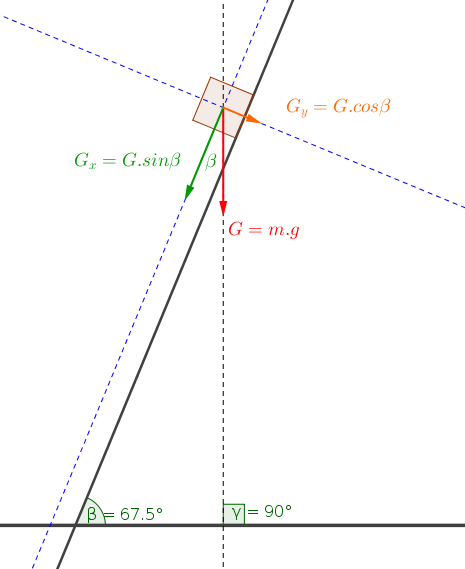
`G_x=mg*sin beta`

`G_x=6*9.81*sin beta`

`color(green)(G_x=54.38 )" "N`

`G_y=mg*cos beta`

`G_y=6*9.81* cos beta`

`color(orange)(G_y=22.52)" " N`

`"since it is perpendicular to the surface ,The " G_y " component causes friction."`

`color(red)(F_f=mu_k*G_y)`

`F_f=2/5*22.52`

`F_f=9" "N`

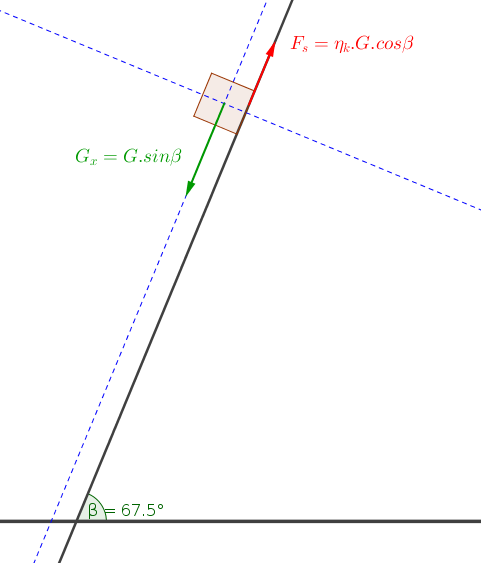
`"Since "G_x " greater than "F_f ," block is sliding down."`
`F_("net")=G_x-F_f=54.38-9`

`F_("net")=45.38 " "N`

`"it is necessary a 45 Newtons of force at opposite direction"`
`"so that it does not slide."`