Frequency of vibration of two masses connected by a spring?
Two masses #m_1# and #m_2# are joined by a spring of spring constant #k# . Show that the frequency of vibration of these masses along the line connecting them is:
#\omega=\sqrt{\frac{k(m_1+m_2)}{m_1m_2}}#
So I have that the distance traveled by #m_1# can be represented by the function #x_1(t)=Acos(\omega t)# and similarly for the distance traveled by #m_2# is #x_2(t)=Bcos(\omega t)# . The force the spring exerts on these two masses is #-kx_n(t)=m_n\frac{d^2x_n}{dt^2}# . But after, simplifying I have no idea how to combine these two functions.
Two masses
So I have that the distance traveled by
3 Answers
Explanation:
The distance each mass is displaced can be represented by the following
Using the formula for simple harmonic oscillation
Solving we get
Plugging this into the first equation for simple harmonic oscillation we get
Simplify to get
This problem has only 1 dimension, so it seems simple as it is motion along the number line. But there are 2 variables (degrees of freedom).
The Lagrangian is often a safe (lazy) way to extract the DE's.
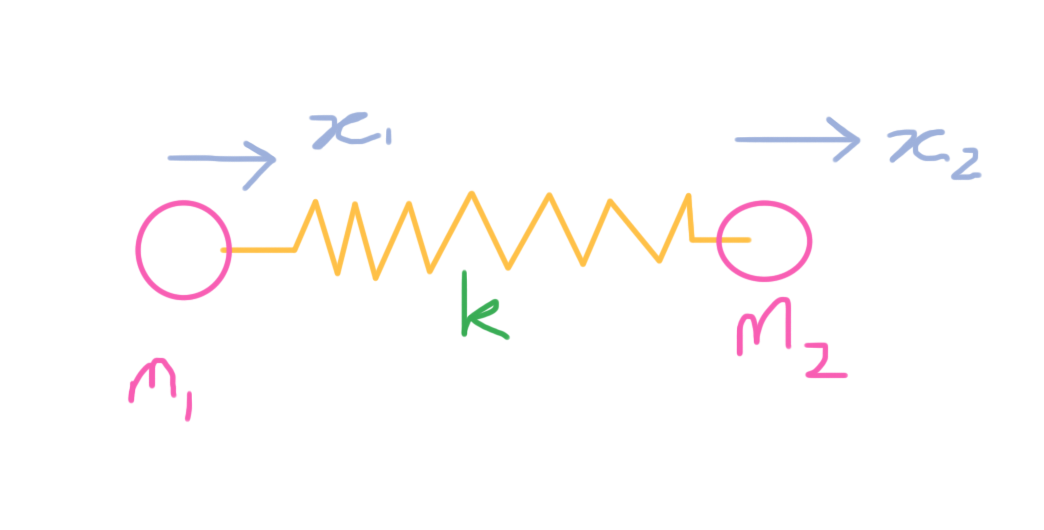
If
Lagrangian
Or:
We can solve that system based upon matrix
-
#lambda_1 = 0, mathbf e_1 = ((1),(1))# -
#lambda_2 = - k(m_1 + m_2)/(m_1m_2), mathbf e_2 = ((- m_2/m_1),(1))#
This is the diagonalisation trick. Because:
-
S is the matrix of eigenvectors =
# ((1, -m_2/m_1),(1, 1))# -
#Lambda# is the diagonal matrix of eigenvalues#= ((0,0),(0, - k(m_1 + m_2)/(m_1m_2)))#
Then:
Pre-multiply both sides by
And if we make linear transform:
-
#triangle implies u_1(t) = alpha t + beta# , with#alpha, beta# as some sundry constants -
and with
#omega^2 = k(m_1 + m_2)/(m_1m_2) # , then#square implies u_2(t) = A cos ( omega t + phi)#
To understand what this really means, we go back to
So:
-
#u_1 = (m_1 x_1 + m_2 x_2)/(m_1 + m_2) # ; and so the dimension on the number line that#u_1# measures is either stationary or moving at constant velocity. That makes sense. There are no external forces on this system. And#u_1# is a recipe for the Centre of mass of the system. It's just minding it's own business. -
#u_2 = ( m_1)/(m_1 + m_2)( x_2 - x_1)# . This is a recipe for the actual oscillation within the system, that is based upon the relative displacement of the masses, and ergo the spring constant and the particles masses.
See below.
Explanation:
For each mass we have
The movement is one dimensional so multiplying by
now subtracting the second from the first
now if
then after substitution and simplification
so



