The point #P(alpha,beta)# lies on the curve #C# with equation #f(x)= 1/3x+12/x# such that #alpha>0, alpha≠6#. The normal at #P# only crosses #C# once. How do I find the exact value of #alpha#?

3 Answers
Steve M
May 5, 2017

There is no such point

Explanation:

Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. The normal is perpendicular to the tangent so the product of their gradients is #-1#

We have:

# f(x) = x/3+12/x \ \ \ \ ..... (star)#

# " " = (x^2+36)/(3x) #

First we find the coordinate #beta#; At #P(alpha,beta)# we have:

# beta = f(alpha) #
# \ \ = (alpha^2+36)/(3alpha) #

Then differentiating #(star)# wrt #x# gives us:

# f'(x) = 1/3-12/x^2 #

# " " = (x^2-36)/(3x^2) #

So at the point #P(alpha,beta)# the gradient of the tangent is given by:

# m_T = f'(alpha) #
# " " = (alpha^2-36)/(3alpha^2) #

Hence, the gradient of the normal at #P(alpha,beta)# is given by:

# m_N = -1/m_T #
# " " = -1/((alpha^2-36)/(3alpha^2)) #
# " " = -(3alpha^2)/(alpha^2-36) \ \ \ \ because alpha != 6#

So the normal passes through #P(alpha,beta)# and has gradient #m_N#, so using the point/slope form #y-y_1=m(x-x_1)# the equation of the normal at #P(alpha,beta)# is:

# y-beta = -(3alpha^2)/(alpha^2-36) (x - alpha) #

# :. y= (3alpha^2(alpha-x))/(alpha^2-36) + (alpha^2+36)/(3alpha) #

# :. y= (9alpha^3(alpha-x) + (alpha^2+36)(alpha^2-36))/((3alpha)(alpha^2-36)) #

# :. y= (9alpha^4-9alpha^3x + alpha^4-1296)/((3alpha)(alpha^2-36)) #

# :. y = (10alpha^4-9alpha^3x -1296)/((3alpha)(alpha^2-36)) #

This normal at #P# will cross the original curve #y=f(x)# when we have a simultaneous solution of both of the equations:

# { (y = (x^2+36)/(3x), "(The Function)" ), ( y = (10alpha^4-9alpha^3x -1296)/((3alpha)(alpha^2-36)), "(The Normal)" ) :} #

i.e. a solutions of:

# (x^2+36)/(3x) = (10alpha^4-9alpha^3x -1296)/((3alpha)(alpha^2-36)) #

# :. (x^2+36)/(x) = (10alpha^4-9alpha^3x -1296)/(alpha^3-36alpha) #

# :. (x^2+36)(alpha^3-36alpha) = (10alpha^4-9alpha^3x -1296)x #

# :. alpha^3x^2-36alphax^2+36alpha^3-1296alpha = 10alpha^4x-9alpha^3x^2 -1296x #

# :. alpha^3x^2-36alphax^2+36alpha^3-1296alpha - 10alpha^4x+9alpha^3x^2 +1296x =0#

# :. (10alpha^3-36alpha)x^2 + (1296- 10alpha^4)x+(36alpha^3-1296alpha) = 0#

# :. (5alpha^3-18alpha)x^2 + (648- 5alpha^4)x+(18alpha^3-648alpha) = 0#

This is a quadratic in #x#, and so either has:

  • one repeated real solution
  • two unique real solutions
  • two complex solutions

We want our Normal to touch the original curve just once, and therefore we require one repeated real solution, and so the discriminant, #Delta=b^2-4ac# of the quadratic must be zero, this requires:

# (648- 5alpha^4)^2-4(5alpha^3-18alpha)(18alpha^3-648alpha) = 0#

# :. 419904-6480alpha^4+25alpha^8 - 4(90alpha^6-3240alpha^4-324alpha^4+11664alpha^2) = 0#

# :. 419904-6480alpha^4+25alpha^8 -360alpha^6+14256alpha^4-46656alpha^2 = 0#

# :. 25alpha^8-360alpha^6+7776alpha^4-46656alpha^2 +419904= 0#

# :. (5alpha^4-36alpha^2+648)^2= 0#

# :. 5alpha^4-36alpha^2+648= 0#

And for this quadratic equation in #alpha^2#, we note that its discriminant is:

# Delta = (-36)^2-4(5)(648) #
# \ \ \ = 1296-12960 #
# \ \ \ = -11664 #
# \ \ \ < 0 #

There are no real solutions for #alpha^2#, and therefore no real solutions for #alpha#

Thus the premise of the original question is false, and there is no such point #P(alpha,beta)# that satisfies the given condition.

Cesareo R.
May 6, 2017

#alpha = 3 sqrt[2/5]#

Explanation:

The function

#f(x) = x/3+12/x# has two leafs and two asymptotes . One vertical at #x = 0# and other slanted which is

#y=x/3#

Building a normal line in the positive-right leaf, we have a point which is it's minimum point, such that the normal does intersect #f(x)# only once. This point is at

#(df)/(dx)=1/3 - 12/x_0^2=0# giving #x_0 = pm 6#

The only non intersecting normal for #x ne 6# is given at

#-1/((df)/(dx)) = 1/3#

or

#(df)/(dx) = -3#

or

#1/3 +3- 12/x_1^2 = 0#

so for #x_1 =pm3 sqrt[2/5]#

The normal equations are then

#y_1=sqrt[2/5] + 2 sqrt[10] + 1/3 (x-3 sqrt[2/5] )#
#y_2=-sqrt[2/5] - 2 sqrt[10] + 1/3 (x+3 sqrt[2/5] )#

So, we can construct four normal lines which do not intersect the other leaf. The verticals and the slanted.

Attached a plot showing the normal lines at #x = x_1 = pm3 sqrt[2/5]#

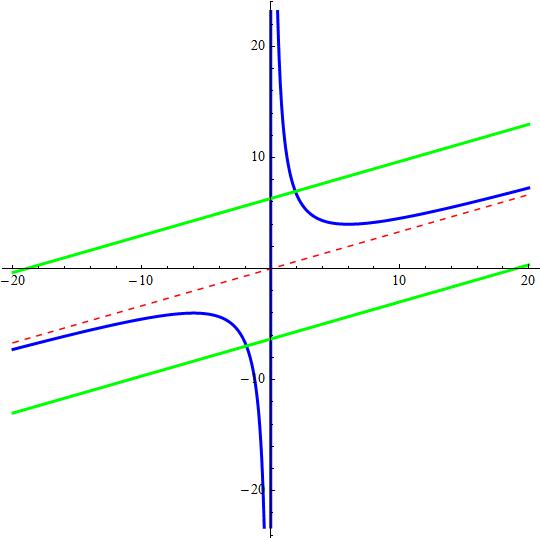
enter image source here

Cesareo R.
May 6, 2017

See below.

Explanation:

Another approach.

Defining #p = (x,y)# and #p_0=(alpha,beta)#

#f(x,y)=f(p) = y-x/3-12/x =0#

we have

#vec n_0 = grad f(p_0) = (-1/3 + 12/alpha^2, 1)#

so the normal line passing by #p_0# is

#L_n->p=p_0+lambda vec n_0# or

#{(alpha -lambda/3 + (12 lambda)/alpha^2=0),(12/alpha + alpha/3 + lambda=0):}#

Now doing

#f(p_0+lambda vec n_0)=0# and solving for #lambda# we have

#{(lambda = 0), (lambda= ( 3 alpha (648 - 36 alpha^2 + 5 alpha^4))/( 648 - 198 alpha^2 + 5 alpha^4)):} #

So we have the two potential intersections within the normal and the function #f(p)=0#

One of them is obviously for #lambda = 0#. If this is the only intersection, then

#lambda= ( 3 alpha (648 - 36 alpha^2 + 5 alpha^4))/( 648 - 198 alpha^2 + 5 alpha^4)#

must be not a real number. This is satisfied when

#648 - 198 alpha^2 + 5 alpha^4=0# with the solutions

#alpha = (-6,6,-3 sqrt[2/5],3 sqrt[2/5])#

so there are solutions located at #alpha = pm 3 sqrt[2/5]#

Related questions
Impact of this question
1330 views around the world
You can reuse this answer
Creative Commons License