Question

How do I find the volume of this integral?

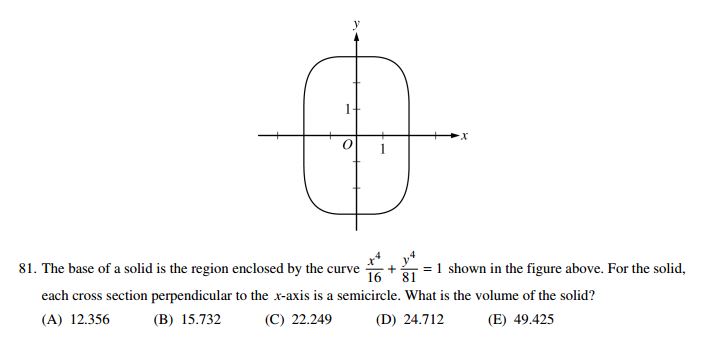
I tried to do it but I got 11.4 something

Answer 1

(E) 49.425

Explanation:

Since we are dealing with cross-sections perpendicular to the `x`-axis, we should put the equation into "`y` equals" form.

`y^4/81=1-x^4/16=(16-x^4)/16`

`y^4=81/16(16-x^4)`

`y=pm3/2(16-x^4)^(1/4)`

Since the base of the solid is not given by a function, we see it is the union of the positive and negative versions of the same function, symmetric about the `x`-axis.

If the entire cross section is the diameter of a semicircle, then the radius of the circle is given by `r=3/2(16-x^4)^(1/4)`.

The area of this semicircle is one-half the area of the circle with radius `r`. So, the area of each semicircle is `1/2pir^2`.

Note that `1/2pir^2=pi/2(3/2(16-x^4))^2=(9pi)/8(16-x^4)^(1/2)`.

So, we want to sum this area across the entire span of the solid.

The solid "begins" and "ends" where `y=0`. This is when `16-x^4=0`, or `x=pm2`.

Then volume of the solid is then the sum of all the semicircles' areas from `x=-2` to `x=2`, or:

`int_(-2)^2(9pi)/8(16-x^4)^(1/2)dx~~49.425`