Question

How do you solve the system of equations `-6x+2y=-16` and `5x+5y=-20` by graphing?

Answer 1

Evaluate some sample solution points for each equation; plot those points; draw a line through the sample points for each equation; where the line intersect is the system solution coordinates.

Explanation:

Here are my sample points:
`color(white)("XXX")color(green)(-6x+2y=-16)`
#color(white)("XXXXX"){: (color(green)(ul(x)),color(white)("XX"),color(green)(ul(y))), (color(green)0,,color(green)(-8)), (color(green)1,,color(green)(-5)), (color(green)(-1),,-11) :}#

`color(white)("XXX")color(magenta)(5x+5y=20)`
#color(white)("XXXXX"){: (color(magenta)(ul(x)),color(white)("XX"),color(magenta)(ul(y))), (color(magenta)0,,color(magenta)4), (color(magenta)1,,color(magenta)3), (color(magenta)(-1),,color(magenta)5) :}#

After plotting each set of coordinates and drawing a line through each set, my graph looks like:

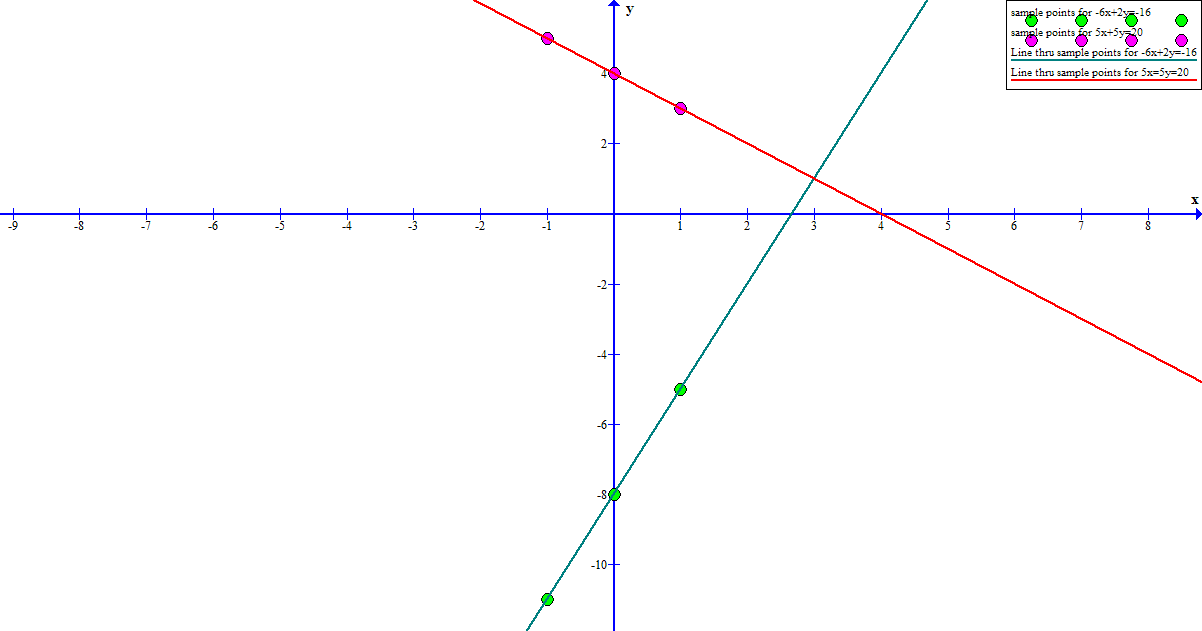
The point of intersection appears to be (at least approximately)
`color(white)("XXX")(x,y)=(3,1)`