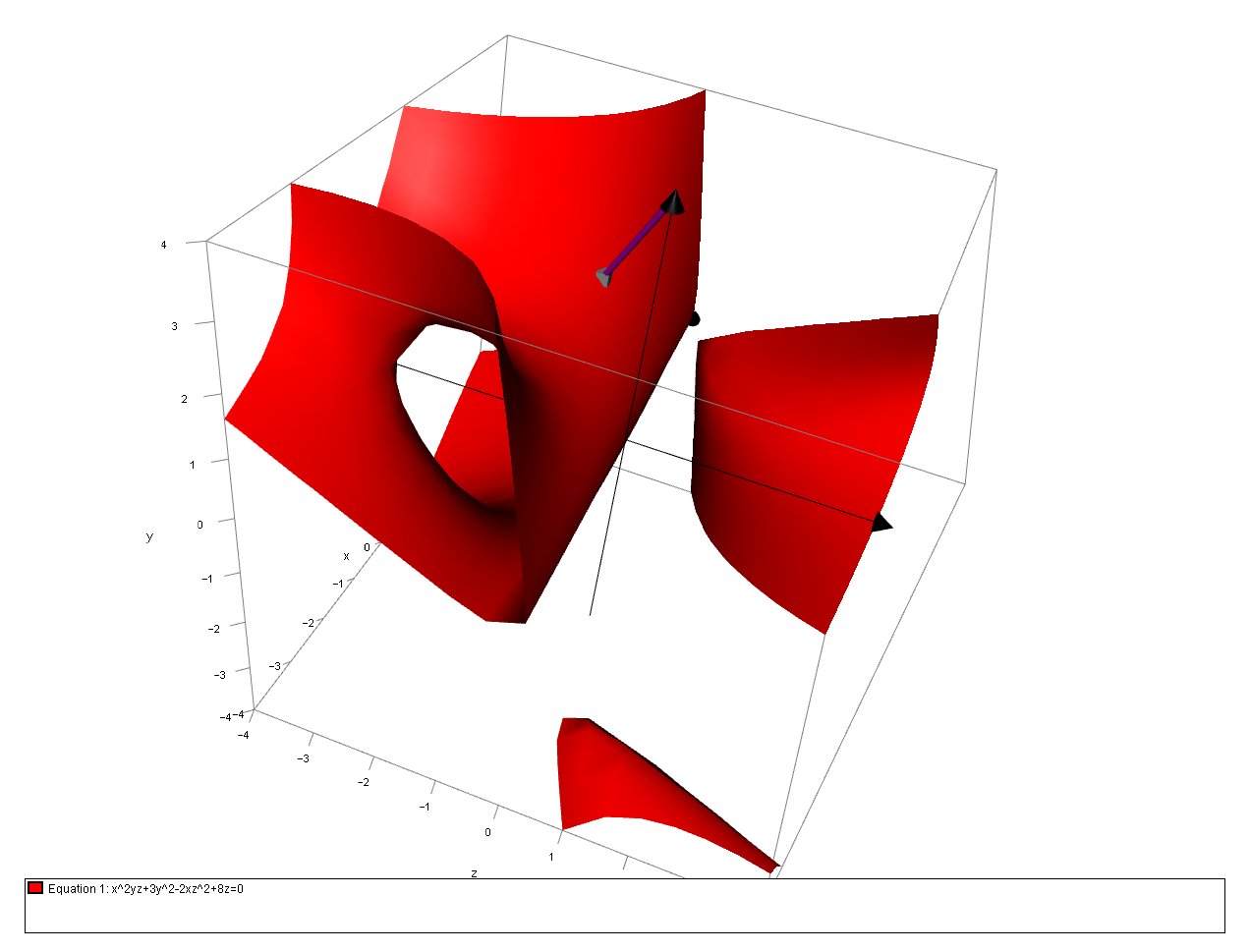
Find the normal vector of the tangent plane to #x^2yz+3y^2-2xz^2+8z=0 # at #(1,2,-1)# ?
1 Answer
# -6hat(i) +12hat(j)+14hat(k) #
Explanation:
First we rearrange the equation of the surface into the form
# x^2yz+3y^2-2xz^2+8z=0 #
And so we define our surface function,
# f(x,y,z) = x^2yz+3y^2-2xz^2+8z #
In order to find the normal at any particular point in vector space we use the Del, or gradient operator:
# grad f(x,y,z) = (partial f)/(partial x) hat(i) + (partial f)/(partial y) hat(j) + (partial f)/(partial z) hat(k) #
remember when partially differentiating that we differentiate wrt the variable in question whilst treating the other variables as constant. And so:
# grad f = ((partial)/(partial x) (x^2yz+3y^2-2xz^2+8z))hat(i) + #
# " " ((partial)/(partial y) (x^2yz+3y^2-2xz^2+8z))hat(j) + #
# " " ((partial)/(partial z) (x^2yz+3y^2-2xz^2+8z))hat(k) #
# " "= (2xyz-2z^2)hat(i) + (x^2z+6y)hat(j) + (x^2y-4x+8)hat(k) #
So for the particular point
# grad f(1,2,-11) = (-4-2)hat(i) +(-1+12)hat(j) +(2-4+8)hat(k) #
# " " = -6hat(i) +12hat(j)+14hat(k) #
We can confirm this graphically: Here is the surface with the normal vector: