Question

If given: `Sn(s) + Cl_2(g) -> SnCl_2(s)`, `DeltaH = -325 kJ` and `SnCl_2(s) + Cl_2(g) -> SnCl_4(l)`, `DeltaH = -186 kJ`, what is `DeltaH` for this reaction? `Sn(s) + 2Cl_2(g) -> SnCl_4(l)`

Answer 1

Use Hess's law to simplify

Explanation:

First of all, write out the equations

`Sn(s) + Cl_"2"(g) -> SnCl_"2"(s)` `DeltaH = -325kJ`

`SnCl_"2"(s) + Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -186kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

Next, we will rework the two equations on top. What we will do determines the answer for the problem. First, we will flip around equations (if necessary) so that the products of the equation or reactants of the top equations will be the same products and reactants as the very bottom equation.

Next, we will change the coefficients of the top two equations to match those of the bottom equation. Let's work it out below:

`Sn(s) + Cl_"2"(g) -> SnCl_"2"(s)` `DeltaH = -325kJ`

`SnCl_"2"(s) + Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -186kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

It seems in this equation, however, the coefficients are set correctly and the equations do not need to be flipped. Now we will do the last step, which is canceling out unneeded products/reactants to get an equation identical to the bottom equation. the "x" is attached to those products/reactants that are canceled out

`Sn(s) + Cl_"2"(g) ->` x(`SnCl_"2"(s))` `DeltaH = -325kJ`

x(`SnCl_"2"(s)) + Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -186kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

=

`Sn(s) + Cl_"2"(g) -> )` `DeltaH = -325kJ`

`Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -186kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

Now, when we add the two equations together to equal the bottom equation, we also add the `DeltaH` for each equation together

           #DeltaH = -325kJ#

`Sn(s) + Cl_"2"(g) + Cl_"2"(g) -> SnCl_"4"(l)`
`DeltaH = -186kJ + -325kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

Now combine like terms to finish the problem

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -511kJ`

_- - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = ???`

See how the two equations are now exactly the same? Well, so are the `DeltaH` values!. So, now your final answer is:

`Sn(s) + 2Cl_"2"(g) -> SnCl_"4"(l)` `DeltaH = -511kJ`

Final answer: `-511kJ`

Answer 2

`sf(DeltaH=-511color(white)(x)kJ)`

Explanation:

Hess' Law states that the overall enthalpy change of a chemical reaction is independent of the route taken. This is a consequence of The Conservation of Energy.

I have set up a Hess Cycle:

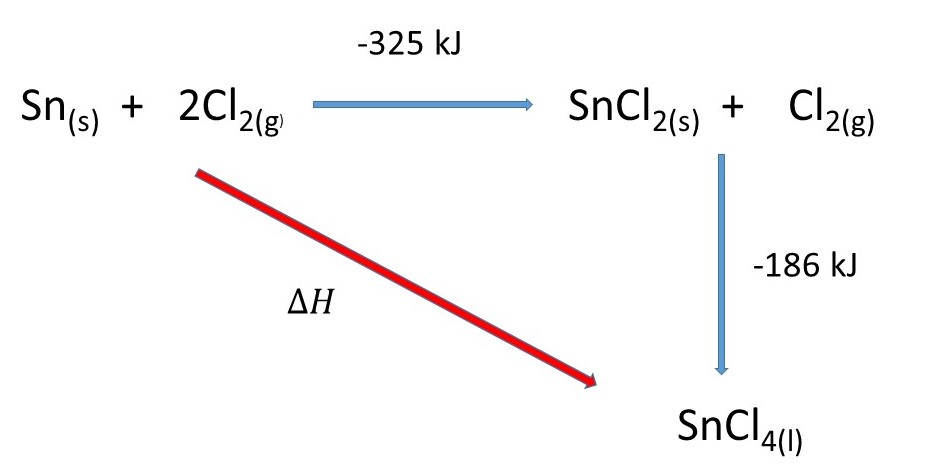
Applying Hess' Law you can say that the enthalpy change of the `sf(color(red)(red))` route is equal to the enthalpy change of the `sf(color(blue)(blue))` route. This is because the arrows start and finish in the same place.

We can say:

`sf(DeltaH=-325-186=-511color(white)(x)kJ)`

For the reaction `sf(Sn_((s))+2Cl_(2(g))rarrSnCl_(4(l))`